| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 to 5 (Before Exercise 8.1) | Exercise 8.1 | Example 6 to 8 (Before Exercise 8.2) |
| Exercise 8.2 | Example 9 to 12 (Before Exercise 8.3) | Exercise 8.3 |
Chapter 8 Introduction To Trigonometry
Welcome to the solutions guide for Chapter 8, "Introduction to Trigonometry," from the latest Class 10 NCERT mathematics textbook for the academic session 2024-25. Trigonometry is a vital branch of mathematics that studies the relationships between the angles and side lengths of triangles, particularly right-angled triangles. It provides powerful tools for indirect measurement and forms the foundation for many concepts in calculus, physics, engineering, navigation, and more. This chapter introduces the fundamental trigonometric ratios and identities. These solutions offer detailed, step-by-step explanations and derivations to help students master these essential concepts and techniques.
The journey into trigonometry begins with defining the six Trigonometric Ratios for an acute angle ($\theta$) within a right-angled triangle. These ratios relate the angle to the lengths of the sides: Opposite, Adjacent, and Hypotenuse relative to the angle $\theta$. The solutions clearly define:
- $\sin \theta = \frac{\text{Opposite}}{\text{Hypotenuse}}$
- $\cos \theta = \frac{\text{Adjacent}}{\text{Hypotenuse}}$
- $\tan \theta = \frac{\text{Opposite}}{\text{Adjacent}}$
- $\text{cosec } \theta = \frac{1}{\sin \theta} = \frac{\text{Hypotenuse}}{\text{Opposite}}$
- $\sec \theta = \frac{1}{\cos \theta} = \frac{\text{Hypotenuse}}{\text{Adjacent}}$
- $\cot \theta = \frac{1}{\tan \theta} = \frac{\text{Adjacent}}{\text{Opposite}}$
Specific angles occur frequently in applications, and their trigonometric ratio values are important to know. The solutions provide methods for deriving or recalling the values of these ratios for standard angles: $0^\circ, 30^\circ, 45^\circ, 60^\circ,$ and $90^\circ$. Step-by-step calculations are shown for evaluating various expressions that involve combinations of these standard angle ratios, emphasizing correct substitution and arithmetic simplification.
A significant focus of this chapter is on Trigonometric Identities. These are equations involving trigonometric ratios that hold true for all values of the angle(s) for which the ratios are defined. The cornerstone identities are the three Pythagorean Identities:
- $\sin^2\theta + \cos^2\theta = 1$
- $1 + \tan^2\theta = \sec^2\theta$
- $1 + \cot^2\theta = \text{cosec }^2\theta$
Regarding the rationalized syllabus for 2024-25, Chapter 8, "Introduction to Trigonometry," has seen a significant adjustment. The section dealing with trigonometric ratios of complementary angles (like $\sin(90^\circ - \theta) = \cos \theta$, etc.) and all related exercises have been removed. The curriculum now focuses primarily on the definition of trigonometric ratios, values for standard angles (0°, 30°, 45°, 60°, 90°), and proving identities using the three fundamental Pythagorean identities. By diligently studying these focused solutions, students can gain a firm grasp of the basic trigonometric ratios, memorize standard angle values, and develop essential skills in proving trigonometric identities using logical algebraic manipulation.
Example 1 to 5 (Before Exercise 8.1)
Example 1. Given tan A = $\frac{4}{3}$ , find the other trigonometric ratios of the angle A.
Answer:
Given:
$ \tan \text{A} = \frac{4}{3} $
To Find:
The other trigonometric ratios of angle A, namely $ \sin \text{A}, \cos \text{A}, \text{cosec } \text{A}, \sec \text{A}, \cot \text{A} $.
Construction Required:
Consider a right-angled triangle ABC, right-angled at B, with $ \angle\text{BAC} = \text{A} $. The side opposite to angle A is BC, the side adjacent to angle A is AB, and the hypotenuse is AC.
Solution:
We are given that $ \tan \text{A} = \frac{4}{3} $.
The tangent of an angle in a right-angled triangle is defined as the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle.
$\tan \text{A} = \frac{\text{Side opposite to angle A}}{\text{Side adjacent to angle A}}$
(Definition of tangent)
In our triangle ABC, with $ \angle\text{B} = 90^\circ $ and $ \angle\text{A} $ at vertex A:
$\tan \text{A} = \frac{\text{BC}}{\text{AB}}$
So, we have $ \frac{\text{BC}}{\text{AB}} = \frac{4}{3} $.
We can assume that the length of the side opposite to angle A, BC, is $4k$, and the length of the side adjacent to angle A, AB, is $3k$, where $k$ is a positive constant.
$ \text{BC} = 4k $
$ \text{AB} = 3k $
Now, we need to find the length of the hypotenuse AC using the Pythagorean theorem in the right-angled triangle ABC:
$\text{AC}^2 = \text{AB}^2 + \text{BC}^2$
(Pythagorean theorem)
Substitute the values of AB and BC:
$ \text{AC}^2 = (3k)^2 + (4k)^2 $
$ \text{AC}^2 = 9k^2 + 16k^2 $
$ \text{AC}^2 = 25k^2 $
Take the square root of both sides to find AC:
$ \text{AC} = \sqrt{25k^2} = \sqrt{25} \sqrt{k^2} = 5k $
So, the lengths of the sides of the triangle are:
$ \text{AB} = 3k $ (Adjacent side)
$ \text{BC} = 4k $ (Opposite side)
$ \text{AC} = 5k $ (Hypotenuse)
Now we can find the other trigonometric ratios using their definitions:
Sine of angle A:
$\sin \text{A} = \frac{\text{Side opposite to angle A}}{\text{Hypotenuse}} = \frac{\text{BC}}{\text{AC}} = \frac{4k}{5k} = \frac{4}{5}$
Cosine of angle A:
$\cos \text{A} = \frac{\text{Side adjacent to angle A}}{\text{Hypotenuse}} = \frac{\text{AB}}{\text{AC}} = \frac{3k}{5k} = \frac{3}{5}$
Cosecant of angle A (reciprocal of sin A):
$\text{cosec } \text{A} = \frac{1}{\sin \text{A}} = \frac{\text{Hypotenuse}}{\text{Side opposite to angle A}} = \frac{\text{AC}}{\text{BC}} = \frac{5k}{4k} = \frac{5}{4}$
Secant of angle A (reciprocal of cos A):
$\sec \text{A} = \frac{1}{\cos \text{A}} = \frac{\text{Hypotenuse}}{\text{Side adjacent to angle A}} = \frac{\text{AC}}{\text{AB}} = \frac{5k}{3k} = \frac{5}{3}$
Cotangent of angle A (reciprocal of tan A):
$\cot \text{A} = \frac{1}{\tan \text{A}} = \frac{\text{Side adjacent to angle A}}{\text{Side opposite to angle A}} = \frac{\text{AB}}{\text{BC}} = \frac{3k}{4k} = \frac{3}{4}$
Answer:
Given $ \tan \text{A} = \frac{4}{3} $, the other trigonometric ratios of angle A are:
$ \sin \text{A} = \frac{4}{5} $
$ \cos \text{A} = \frac{3}{5} $
$ \text{cosec } \text{A} = \frac{5}{4} $
$ \sec \text{A} = \frac{5}{3} $
$ \cot \text{A} = \frac{3}{4} $
Example 2. If ∠B and ∠Q are acute angles such that sin B = sin Q, then prove that ∠B = ∠Q.
Answer:
Given:
$ \angle \text{B} $ and $ \angle \text{Q} $ are acute angles.
$ \sin \text{B} = \sin \text{Q} $.
To Prove:
$ \angle \text{B} = \angle \text{Q} $.
Construction Required:
Consider two right-angled triangles, $\triangle$ ABC and $\triangle$ PQR, such that $\angle$ A = $90^\circ$ and $\angle$ P = $90^\circ$. Let $\angle$ B be an acute angle in $\triangle$ ABC and $\angle$ Q be an acute angle in $\triangle$ PQR.
Proof:
In the right-angled triangle ABC, with $ \angle \text{A} = 90^\circ $, the trigonometric ratio $ \sin \text{B} $ is defined as the ratio of the side opposite to angle B to the hypotenuse.
$\sin \text{B} = \frac{\text{Side opposite to angle B}}{\text{Hypotenuse}} = \frac{\text{AC}}{\text{BC}}$
In the right-angled triangle PQR, with $ \angle \text{P} = 90^\circ $, the trigonometric ratio $ \sin \text{Q} $ is defined as the ratio of the side opposite to angle Q to the hypotenuse.
$\sin \text{Q} = \frac{\text{Side opposite to angle Q}}{\text{Hypotenuse}} = \frac{\text{PR}}{\text{QR}}$
We are given that $ \sin \text{B} = \sin \text{Q} $.
Therefore,
$\frac{\text{AC}}{\text{BC}} = \frac{\text{PR}}{\text{QR}}$
We can rearrange this proportion as:
$\frac{\text{AC}}{\text{PR}} = \frac{\text{BC}}{\text{QR}}$
Let this common ratio be $ k $.
$\frac{\text{AC}}{\text{PR}} = \frac{\text{BC}}{\text{QR}} = k$
... (i)
From equation (i), we have $ \text{AC} = k \cdot \text{PR} $ and $ \text{BC} = k \cdot \text{QR} $.
Now, let's use the Pythagorean theorem in both triangles.
In $\triangle$ ABC, by Pythagorean theorem:
$\text{AB}^2 + \text{AC}^2 = \text{BC}^2$
Rearranging to find $ \text{AB}^2 $:
$\text{AB}^2 = \text{BC}^2 - \text{AC}^2$
Substitute $ \text{BC} = k \cdot \text{QR} $ and $ \text{AC} = k \cdot \text{PR} $ into this equation:
$ \text{AB}^2 = (k \cdot \text{QR})^2 - (k \cdot \text{PR})^2 $
$ \text{AB}^2 = k^2 \cdot \text{QR}^2 - k^2 \cdot \text{PR}^2 $
$ \text{AB}^2 = k^2 (\text{QR}^2 - \text{PR}^2) $
In $\triangle$ PQR, by Pythagorean theorem:
$\text{PQ}^2 + \text{PR}^2 = \text{QR}^2$
Rearranging to find $ \text{PQ}^2 $:
$\text{PQ}^2 = \text{QR}^2 - \text{PR}^2$
Substitute $ (\text{QR}^2 - \text{PR}^2) = \text{PQ}^2 $ into the equation for $ \text{AB}^2 $:
$\text{AB}^2 = k^2 (\text{PQ}^2)$
Taking the square root of both sides (since length must be positive):
$\text{AB} = \sqrt{k^2 \cdot \text{PQ}^2} = k \cdot \text{PQ}$
This gives us the ratio of the third pair of corresponding sides:
$\frac{\text{AB}}{\text{PQ}} = k$
... (ii)
From equations (i) and (ii), we see that the ratio of all three pairs of corresponding sides of $\triangle$ ABC and $\triangle$ PQR is equal:
$\frac{\text{AC}}{\text{PR}} = \frac{\text{BC}}{\text{QR}} = \frac{\text{AB}}{\text{PQ}}$
Since the ratios of the corresponding sides are equal, the two triangles are similar by the SSS similarity criterion.
$\triangle\text{ABC} \sim \triangle\text{PQR}$
When two triangles are similar, their corresponding angles are equal.
Therefore, the angle B in $\triangle$ ABC must be equal to the corresponding angle Q in $\triangle$ PQR.
$\angle\text{B} = \angle\text{Q}$
(Corresponding angles of similar triangles)
Hence, proved.
Example 3. Consider ∆ ACB, right-angled at C, in which AB = 29 units, BC = 21 units and ∠ABC = θ (see Fig. 8.10). Determine the values of
(i) cos2 θ + sin2 θ,
(ii) cos2 θ – sin2 θ.

Answer:
Given:
In $\triangle$ACB, right-angled at C,
AB = 29 units
BC = 21 units
$\angle$ABC = $\theta$
To Find:
(i) $\cos^2 \theta + \sin^2 \theta$
(ii) $\cos^2 \theta - \sin^2 \theta$
Solution:
In $\triangle$ACB, by Pythagoras theorem, we have:
$AC^2 + BC^2 = AB^2$
(Pythagoras theorem)
$AC^2 + (21)^2 = (29)^2$
$AC^2 + 441 = 841$
$AC^2 = 841 - 441$
$AC^2 = 400$
$AC = \sqrt{400} = 20$ units.
Now, in $\triangle$ACB, with respect to angle $\theta$ at B:
Perpendicular (Opposite side) = AC = 20
Base (Adjacent side) = BC = 21
Hypotenuse = AB = 29
We have:
$\sin \theta = \frac{\text{Perpendicular}}{\text{Hypotenuse}} = \frac{AC}{AB} = \frac{20}{29}$
$\cos \theta = \frac{\text{Base}}{\text{Hypotenuse}} = \frac{BC}{AB} = \frac{21}{29}$
Now, we can find $\sin^2 \theta$ and $\cos^2 \theta$:
$\sin^2 \theta = \left(\frac{20}{29}\right)^2 = \frac{20^2}{29^2} = \frac{400}{841}$
$\cos^2 \theta = \left(\frac{21}{29}\right)^2 = \frac{21^2}{29^2} = \frac{441}{841}$
(i) $\cos^2 \theta + \sin^2 \theta$
$\cos^2 \theta + \sin^2 \theta = \frac{441}{841} + \frac{400}{841}$
$= \frac{441 + 400}{841}$
$= \frac{841}{841}$
$= 1$
(ii) $\cos^2 \theta - \sin^2 \theta$
$\cos^2 \theta - \sin^2 \theta = \frac{441}{841} - \frac{400}{841}$
$= \frac{441 - 400}{841}$
$= \frac{41}{841}$
Example 4. In a right triangle ABC, right-angled at B, if tan A = 1, then verify that
2 sin A cos A = 1.
Answer:
Given:
In a right-angled triangle ABC, the right angle is at B ($ \angle \text{B} = 90^\circ $).
The tangent of angle A is given as $ \tan \text{A} = 1 $.
To Verify:
That $ 2 \sin \text{A} \cos \text{A} = 1 $.
Construction Required:
Draw a right-angled triangle ABC, with the right angle at vertex B. Label the angle at vertex A as A.
Solution:
In the right triangle ABC, we are given that $ \tan \text{A} = 1 $.
The definition of the tangent of an angle in a right triangle is the ratio of the length of the side opposite to the angle to the length of the side adjacent to the angle.
$\tan \text{A} = \frac{\text{Side opposite to angle A}}{\text{Side adjacent to angle A}}$
In $\triangle$ ABC, the side opposite to angle A is BC, and the side adjacent to angle A is AB.
$\tan \text{A} = \frac{\text{BC}}{\text{AB}}$
Since $ \tan \text{A} = 1 $, we have:
$\frac{\text{BC}}{\text{AB}} = 1$
This implies that the length of side BC is equal to the length of side AB.
$\text{BC} = \text{AB}$
Let's assume the length of AB (and thus BC) is $ k $, where $ k $ is a positive number. So, $ \text{AB} = k $ and $ \text{BC} = k $.
Now, we need to find the length of the hypotenuse AC using the Pythagorean theorem in the right-angled triangle ABC.
$\text{AC}^2 = \text{AB}^2 + \text{BC}^2$
(Pythagorean theorem)
Substitute the values of AB and BC:
$ \text{AC}^2 = (k)^2 + (k)^2 $
$ \text{AC}^2 = k^2 + k^2 $
$ \text{AC}^2 = 2k^2 $
Taking the square root of both sides (and considering only the positive value for length):
$ \text{AC} = \sqrt{2k^2} = \sqrt{2} \times \sqrt{k^2} = k\sqrt{2} $
Now that we have the lengths of all three sides in terms of $ k $ ($ \text{AB} = k $, $ \text{BC} = k $, $ \text{AC} = k\sqrt{2} $), we can find the values of $ \sin \text{A} $ and $ \cos \text{A} $.
The sine of angle A is the ratio of the opposite side to the hypotenuse:
$\sin \text{A} = \frac{\text{Side opposite to angle A}}{\text{Hypotenuse}} = \frac{\text{BC}}{\text{AC}} = \frac{k}{k\sqrt{2}}$
$ \sin \text{A} = \frac{1}{\sqrt{2}} $
The cosine of angle A is the ratio of the adjacent side to the hypotenuse:
$\cos \text{A} = \frac{\text{Side adjacent to angle A}}{\text{Hypotenuse}} = \frac{\text{AB}}{\text{AC}} = \frac{k}{k\sqrt{2}}$
$ \cos \text{A} = \frac{1}{\sqrt{2}} $
Now, we need to verify the given equation $ 2 \sin \text{A} \cos \text{A} = 1 $.
Substitute the values of $ \sin \text{A} $ and $ \cos \text{A} $ into the left side of the equation:
$ \text{Left Hand Side} = 2 \sin \text{A} \cos \text{A} $
$ = 2 \times \left(\frac{1}{\sqrt{2}}\right) \times \left(\frac{1}{\sqrt{2}}\right) $
Multiply the terms:
$ = 2 \times \left(\frac{1 \times 1}{\sqrt{2} \times \sqrt{2}}\right) $
$ = 2 \times \left(\frac{1}{2}\right) $
$ = \frac{2}{2} $
$ = 1 $
The value of the left side is 1, which is equal to the right side of the equation ($ 1 $).
$ \text{Left Hand Side} = \text{Right Hand Side} $
Thus, $ 2 \sin \text{A} \cos \text{A} = 1 $ is verified.
Example 5. In ∆ OPQ, right-angled at P, OP = 7 cm and OQ – PQ = 1 cm (see Fig. 8.12). Determine the values of sin Q and cos Q.

Answer:
Given:
In $\triangle$OPQ, right-angled at P,
OP = 7 cm
OQ – PQ = 1 cm
To Find:
$\sin Q$ and $\cos Q$
Solution:
We are given OQ – PQ = 1 cm.
This can be written as OQ = 1 + PQ.
In the right triangle $\triangle$OPQ, by the Pythagoras theorem, we have:
$OP^2 + PQ^2 = OQ^2$
(Pythagoras theorem)
Substitute the given value of OP and the relation OQ = 1 + PQ into the equation:
$(7)^2 + PQ^2 = (1 + PQ)^2$
$49 + PQ^2 = 1^2 + 2(1)(PQ) + PQ^2$
$49 + PQ^2 = 1 + 2PQ + PQ^2$
Subtract $PQ^2$ from both sides:
$49 = 1 + 2PQ$
$49 - 1 = 2PQ$
$48 = 2PQ$
$PQ = \frac{48}{2}$
$PQ = 24$ cm
Now, find OQ using the relation OQ = 1 + PQ:
$OQ = 1 + 24$
$OQ = 25$ cm
So, the lengths of the sides of $\triangle$OPQ are OP = 7 cm, PQ = 24 cm, and OQ = 25 cm.
Now, we can find $\sin Q$ and $\cos Q$. For angle Q:
Opposite side = OP = 7 cm
Adjacent side = PQ = 24 cmHypotenuse = OQ = 25 cm
$\sin Q = \frac{\text{Opposite side}}{\text{Hypotenuse}} = \frac{OP}{OQ} = \frac{7}{25}$
$\cos Q = \frac{\text{Adjacent side}}{\text{Hypotenuse}} = \frac{PQ}{OQ} = \frac{24}{25}$
Exercise 8.1
Question 1. In ∆ ABC, right-angled at B, AB = 24 cm, BC = 7 cm. Determine :
(i) sin A, cos A
(ii) sin C, cos C
Answer:
Given:
In $\triangle$ ABC, the right angle is at B ($ \angle \text{B} = 90^\circ $).
The length of side AB = $ 24\text{ cm} $.
The length of side BC = $ 7\text{ cm} $.
To Find:
(i) The values of $ \sin \text{A} $ and $ \cos \text{A} $.
(ii) The values of $ \sin \text{C} $ and $ \cos \text{C} $.
Construction Required:
Draw a right-angled triangle ABC, with the right angle at vertex B. Label the lengths of the sides AB = 24 cm and BC = 7 cm.
Solution:
In the right-angled triangle ABC, we are given the lengths of the two sides AB and BC. To find the trigonometric ratios, we first need to find the length of the hypotenuse AC.
We can use the Pythagoras theorem in $\triangle$ ABC, since it is right-angled at B:
$\text{AC}^2 = \text{AB}^2 + \text{BC}^2$
(Pythagoras theorem)
Substitute the given values of AB and BC:
$ \text{AC}^2 = (24)^2 + (7)^2 $
$ \text{AC}^2 = 576 + 49 $
$ \text{AC}^2 = 625 $
Take the square root of both sides to find the length of AC (we consider the positive root since length is positive):
$ \text{AC} = \sqrt{625} $
We know that $ 25^2 = 625 $.
$ \text{AC} = 25 $ cm
So, the length of the hypotenuse is 25 cm.
(i) Determine $ \sin \text{A} $ and $ \cos \text{A} $:
For angle A, the side opposite to A is BC, the side adjacent to A is AB, and the hypotenuse is AC.
Opposite side (BC) = 7 cm
Adjacent side (AB) = 24 cm
Hypotenuse (AC) = 25 cm
The sine of angle A is the ratio of the opposite side to the hypotenuse:
$ \sin \text{A} = \frac{\text{Side opposite to angle A}}{\text{Hypotenuse}} = \frac{\text{BC}}{\text{AC}} = \frac{7}{25} $
The cosine of angle A is the ratio of the adjacent side to the hypotenuse:
$ \cos \text{A} = \frac{\text{Side adjacent to angle A}}{\text{Hypotenuse}} = \frac{\text{AB}}{\text{AC}} = \frac{24}{25} $
(ii) Determine $ \sin \text{C} $ and $ \cos \text{C} $:
For angle C, the side opposite to C is AB, the side adjacent to C is BC, and the hypotenuse is AC.
Opposite side (AB) = 24 cm
Adjacent side (BC) = 7 cm
Hypotenuse (AC) = 25 cm
The sine of angle C is the ratio of the opposite side to the hypotenuse:
$ \sin \text{C} = \frac{\text{Side opposite to angle C}}{\text{Hypotenuse}} = \frac{\text{AB}}{\text{AC}} = \frac{24}{25} $
The cosine of angle C is the ratio of the adjacent side to the hypotenuse:
$ \cos \text{C} = \frac{\text{Side adjacent to angle C}}{\text{Hypotenuse}} = \frac{\text{BC}}{\text{AC}} = \frac{7}{25} $
Answer:
(i) $ \sin \text{A} = \frac{7}{25} $ and $ \cos \text{A} = \frac{24}{25} $.
(ii) $ \sin \text{C} = \frac{24}{25} $ and $ \cos \text{C} = \frac{7}{25} $.
Question 2. In Fig. 8.13, find tan P – cot R.
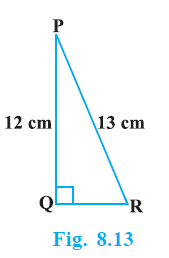
Answer:
Given:
In $\triangle$PQR, right-angled at Q,
PQ = 12 cm
PR = 13 cm
To Find:
$\tan P - \cot R$
Solution:
In right-angled $\triangle$PQR, by Pythagoras theorem, we have:
$PQ^2 + QR^2 = PR^2$
(Pythagoras theorem)
$(12)^2 + QR^2 = (13)^2$
$144 + QR^2 = 169$
$QR^2 = 169 - 144$
$QR^2 = 25$
$QR = \sqrt{25}$
$QR = 5$ cm
Now, we find $\tan P$ and $\cot R$:
For angle P:
Opposite side to angle P = QR = 5 cm
Adjacent side to angle P = PQ = 12 cm
$\tan P = \frac{\text{Opposite side}}{\text{Adjacent side}} = \frac{QR}{PQ} = \frac{5}{12}$
For angle R:
Opposite side to angle R = PQ = 12 cm
Adjacent side to angle R = QR = 5 cm
$\cot R = \frac{\text{Adjacent side}}{\text{Opposite side}} = \frac{QR}{PQ} = \frac{5}{12}$
Now, we calculate $\tan P - \cot R$:
$\tan P - \cot R = \frac{5}{12} - \frac{5}{12}$
$= 0$
Question 3. If sin A = $\frac{3}{4}$ , calculate cos A and tan A.
Answer:
Given:
$\sin A = \frac{3}{4}$
To Find:
$\cos A$ and $\tan A$
Solution:
We are given $\sin A = \frac{3}{4}$.
We know that in a right-angled triangle, $\sin A = \frac{\text{Opposite side to A}}{\text{Hypotenuse}}$.
So, if we consider a right triangle ABC, right-angled at B, where $\angle$A is the angle in question, we can say:
Opposite side (BC) = $3k$
Hypotenuse (AC) = $4k$
where $k$ is a positive constant.
Using the Pythagoras theorem in $\triangle$ABC:
$AB^2 + BC^2 = AC^2$
(Pythagoras theorem)
$AB^2 + (3k)^2 = (4k)^2$
$AB^2 + 9k^2 = 16k^2$
$AB^2 = 16k^2 - 9k^2$
$AB^2 = 7k^2$
$AB = \sqrt{7k^2} = k\sqrt{7}$ (Since length must be positive)
Now, we have the lengths of all three sides in terms of $k$:
Opposite side (BC) = $3k$
Adjacent side (AB) = $k\sqrt{7}$
Hypotenuse (AC) = $4k$
Now we can calculate $\cos A$ and $\tan A$:
$\cos A = \frac{\text{Adjacent side to A}}{\text{Hypotenuse}} = \frac{AB}{AC} = \frac{k\sqrt{7}}{4k} = \frac{\sqrt{7}}{4}$
$\tan A = \frac{\text{Opposite side to A}}{\text{Adjacent side to A}} = \frac{BC}{AB} = \frac{3k}{k\sqrt{7}} = \frac{3}{\sqrt{7}}$
So, $\cos A = \frac{\sqrt{7}}{4}$ and $\tan A = \frac{3}{\sqrt{7}}$.
Question 4. Given 15 cot A = 8, find sin A and sec A.
Answer:
Given:
$15 \cot A = 8$
To Find:
$\sin A$ and $\sec A$
Solution:
We are given $15 \cot A = 8$.
From this, we can write $\cot A = \frac{8}{15}$.
We know that in a right-angled triangle, $\cot A = \frac{\text{Adjacent side to A}}{\text{Opposite side to A}}$.
Let's consider a right triangle ABC, right-angled at B, where $\angle$A is the angle in question.
So, we can take:
Adjacent side (AB) = $8k$
Opposite side (BC) = $15k$
where $k$ is a positive constant.
Using the Pythagoras theorem in $\triangle$ABC:
$AC^2 = AB^2 + BC^2$
(Pythagoras theorem)
$AC^2 = (8k)^2 + (15k)^2$
$AC^2 = 64k^2 + 225k^2$
$AC^2 = 289k^2$
$AC = \sqrt{289k^2}$
$AC = 17k$ (Since length must be positive)
Now, we have the lengths of all three sides in terms of $k$:
Opposite side (BC) = $15k$
Adjacent side (AB) = $8k$
Hypotenuse (AC) = $17k$
Now we can calculate $\sin A$ and $\sec A$:
$\sin A = \frac{\text{Opposite side to A}}{\text{Hypotenuse}} = \frac{BC}{AC} = \frac{15k}{17k} = \frac{15}{17}$
$\sec A = \frac{\text{Hypotenuse}}{\text{Adjacent side to A}} = \frac{AC}{AB} = \frac{17k}{8k} = \frac{17}{8}$
So, $\sin A = \frac{15}{17}$ and $\sec A = \frac{17}{8}$.
Question 5. Given sec θ = $\frac{13}{12}$ , calculate all other trigonometric ratios.
Answer:
Given:
$\sec \theta = \frac{13}{12}$
To Find:
All other trigonometric ratios ($\sin \theta$, $\cos \theta$, $\tan \theta$, $\cot \theta$, $\text{cosec} \theta$)
Solution:
We are given $\sec \theta = \frac{13}{12}$.
We know that $\sec \theta = \frac{\text{Hypotenuse}}{\text{Adjacent side}}$.
Let's consider a right-angled triangle ABC, right-angled at B, with $\angle$C = $\theta$.
In this triangle:
Hypotenuse (AC) = $13k$
Adjacent side to $\theta$ (BC) = $12k$
where $k$ is a positive constant.
Using the Pythagoras theorem in $\triangle$ABC:
$AB^2 + BC^2 = AC^2$
(Pythagoras theorem)
$AB^2 + (12k)^2 = (13k)^2$
$AB^2 + 144k^2 = 169k^2$
$AB^2 = 169k^2 - 144k^2$
$AB^2 = 25k^2$
$AB = \sqrt{25k^2} = 5k$ (Since length must be positive)
Now we have the lengths of all three sides in terms of $k$ for angle $\theta$ at C:
Opposite side (AB) = $5k$
Adjacent side (BC) = $12k$
Hypotenuse (AC) = $13k$
Now we can calculate the other trigonometric ratios:
$\sin \theta = \frac{\text{Opposite side}}{\text{Hypotenuse}} = \frac{AB}{AC} = \frac{5k}{13k} = \frac{5}{13}$
$\cos \theta = \frac{\text{Adjacent side}}{\text{Hypotenuse}} = \frac{BC}{AC} = \frac{12k}{13k} = \frac{12}{13}$
$\tan \theta = \frac{\text{Opposite side}}{\text{Adjacent side}} = \frac{AB}{BC} = \frac{5k}{12k} = \frac{5}{12}$
$\cot \theta = \frac{1}{\tan \theta} = \frac{12}{5}$
$\text{cosec} \theta = \frac{1}{\sin \theta} = \frac{13}{5}$
Thus, the other trigonometric ratios are:
$\sin \theta = \frac{5}{13}$
$\cos \theta = \frac{12}{13}$
$\tan \theta = \frac{5}{12}$
$\cot \theta = \frac{12}{5}$
$\text{cosec} \theta = \frac{13}{5}$
Question 6. If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.
Answer:
Given:
$\angle$A and $\angle$B are acute angles such that $\cos A = \cos B$.
To Show:
$\angle$A = $\angle$B
Proof:
Let us consider a right-angled triangle ABC, where $\angle$C is the right angle ($90^\circ$). Since $\angle$A and $\angle$B are acute angles, this is a valid construction.
In $\triangle$ABC, the cosine of angle A is defined as:
$\cos A = \frac{\text{Side adjacent to } \angle A}{\text{Hypotenuse}}$
So, $\cos A = \frac{AC}{AB}$
Similarly, the cosine of angle B is defined as:
$\cos B = \frac{\text{Side adjacent to } \angle B}{\text{Hypotenuse}}$
So, $\cos B = \frac{BC}{AB}$
We are given that $\cos A = \cos B$.
$\frac{AC}{AB} = \frac{BC}{AB}$
(Given $\cos A = \cos B$)
Multiplying both sides of the equation by AB (since AB $\neq 0$), we get:
$AC = BC$
In $\triangle$ABC, we have AC = BC. This means that the sides opposite to angles B and A are equal.
By the property of triangles, angles opposite to equal sides are equal.
$\angle A = \angle B$
(Angles opposite to equal sides of a triangle are equal)
Thus, if $\cos A = \cos B$ where A and B are acute angles, then $\angle A = \angle B$.
Question 7. If cot θ = $\frac{7}{8}$ , evaluate :
(i) $\frac{(1 \;+\; sin\; θ) (1 \;-\; sin\; θ)}{(1 \;+\; cos\; θ) (1 \;-\; cos\; θ) }$
(ii) cot2 θ
Answer:
Given:
$ \cot \theta = \frac{7}{8} $
To Evaluate:
(i) $ \frac{(1 \;+\; \sin\; \theta) (1 \;-\; \sin\; \theta)}{(1 \;+\; \cos\; \theta) (1 \;-\; \cos\; \theta) } $
(ii) $ \cot^2 \theta $
Construction Required:
Consider a right-angled triangle ABC, right-angled at B, with $ \angle \text{C} = \theta $. The side opposite to angle $ \theta $ is AB, the side adjacent to angle $ \theta $ is BC, and the hypotenuse is AC.
Solution:
We are given that $ \cot \theta = \frac{7}{8} $.
In a right-angled triangle, the cotangent of an angle is defined as the ratio of the length of the side adjacent to the angle to the length of the side opposite the angle.
$\cot \theta = \frac{\text{Side adjacent to angle } \theta}{\text{Side opposite to angle } \theta}$
In our triangle ABC, with $ \angle \text{B} = 90^\circ $ and $ \angle \text{C} = \theta $:
$\cot \theta = \frac{\text{BC}}{\text{AB}}$
So, we have $ \frac{\text{BC}}{\text{AB}} = \frac{7}{8} $.
We can assume that the length of the side adjacent to angle $ \theta $, BC, is $7k$, and the length of the side opposite to angle $ \theta $, AB, is $8k$, where $k$ is a positive constant.
$ \text{BC} = 7k $
$ \text{AB} = 8k $
Now, we find the length of the hypotenuse AC using the Pythagorean theorem in $\triangle$ ABC:
$\text{AC}^2 = \text{AB}^2 + \text{BC}^2$
(Pythagorean theorem)
$ \text{AC}^2 = (8k)^2 + (7k)^2 $
$ \text{AC}^2 = 64k^2 + 49k^2 $
$ \text{AC}^2 = 113k^2 $
Take the square root of both sides to find AC:
$ \text{AC} = \sqrt{113k^2} = \sqrt{113} \sqrt{k^2} = k\sqrt{113} $ (since length must be positive)
So, the lengths of the sides are:
$ \text{AB} = 8k $ (Opposite side)
$ \text{BC} = 7k $ (Adjacent side)
$ \text{AC} = k\sqrt{113} $ (Hypotenuse)
Now we can find $ \sin \theta $ and $ \cos \theta $:
$ \sin \theta = \frac{\text{Side opposite to angle } \theta}{\text{Hypotenuse}} = \frac{\text{AB}}{\text{AC}} = \frac{8k}{k\sqrt{113}} = \frac{8}{\sqrt{113}} $
$ \cos \theta = \frac{\text{Side adjacent to angle } \theta}{\text{Hypotenuse}} = \frac{\text{BC}}{\text{AC}} = \frac{7k}{k\sqrt{113}} = \frac{7}{\sqrt{113}} $
(i) Evaluate $ \frac{(1 \;+\; \sin\; \theta) (1 \;-\; \sin\; \theta)}{(1 \;+\; \cos\; \theta) (1 \;-\; \cos\; \theta) } $:
The given expression is $ \frac{(1 + \sin \theta)(1 - \sin \theta)}{(1 + \cos \theta)(1 - \cos \theta)} $.
Using the algebraic identity $ (a+b)(a-b) = a^2 - b^2 $ for the numerator and the denominator:
Numerator $ = (1 + \sin \theta)(1 - \sin \theta) = 1^2 - \sin^2 \theta = 1 - \sin^2 \theta $
Denominator $ = (1 + \cos \theta)(1 - \cos \theta) = 1^2 - \cos^2 \theta = 1 - \cos^2 \theta $
The expression becomes $ \frac{1 - \sin^2 \theta}{1 - \cos^2 \theta} $.
Now, substitute the calculated values of $ \sin \theta $ and $ \cos \theta $:
$ \sin \theta = \frac{8}{\sqrt{113}} \implies \sin^2 \theta = \left(\frac{8}{\sqrt{113}}\right)^2 = \frac{8^2}{(\sqrt{113})^2} = \frac{64}{113} $
$ \cos \theta = \frac{7}{\sqrt{113}} \implies \cos^2 \theta = \left(\frac{7}{\sqrt{113}}\right)^2 = \frac{7^2}{(\sqrt{113})^2} = \frac{49}{113} $
Substitute these values into the expression $ \frac{1 - \sin^2 \theta}{1 - \cos^2 \theta} $:
$ \frac{1 - \frac{64}{113}}{1 - \frac{49}{113}} $
Calculate the values in the numerator and denominator:
Numerator: $ 1 - \frac{64}{113} = \frac{113}{113} - \frac{64}{113} = \frac{113 - 64}{113} = \frac{49}{113} $
Denominator: $ 1 - \frac{49}{113} = \frac{113}{113} - \frac{49}{113} = \frac{113 - 49}{113} = \frac{64}{113} $
Now, divide the numerator by the denominator:
$ \frac{\frac{49}{113}}{\frac{64}{113}} = \frac{49}{113} \times \frac{113}{64} $
$ = \frac{49}{\cancel{113}} \times \frac{\cancel{113}}{64} $
$ = \frac{49}{64} $
Thus, $ \frac{(1 \;+\; \sin\; \theta) (1 \;-\; \sin\; \theta)}{(1 \;+\; \cos\; \theta) (1 \;-\; \cos\; \theta) } = \frac{49}{64} $.
(ii) Evaluate $ \cot^2 \theta $:
We are given that $ \cot \theta = \frac{7}{8} $.
To evaluate $ \cot^2 \theta $, we simply square the value of $ \cot \theta $:
$ \cot^2 \theta = (\cot \theta)^2 = \left(\frac{7}{8}\right)^2 $
$ = \frac{7^2}{8^2} = \frac{49}{64} $
Answer:
(i) $ \frac{(1 \;+\; \sin\; \theta) (1 \;-\; \sin\; \theta)}{(1 \;+\; \cos\; \theta) (1 \;-\; \cos\; \theta) } = \frac{49}{64} $
(ii) $ \cot^2 \theta = \frac{49}{64} $
Question 8. If 3 cot A = 4, check whether $\frac{1\;-\;tan^{2}A}{1\;+\;tan^{2}A}$ = cos2 A - sin2 A or not.
Answer:
Given:
$3 \cot A = 4$
To Check:
Whether $\frac{1\;-\;\tan^{2}A}{1\;+\;\tan^{2}A}$ = $\cos^2 A - \sin^2 A$
Solution:
We are given $3 \cot A = 4$.
From this, we get $\cot A = \frac{4}{3}$.
We know that in a right-angled triangle, $\cot A = \frac{\text{Adjacent side to A}}{\text{Opposite side to A}}$.
Let's consider a right triangle ABC, right-angled at B, where $\angle$A is the angle in question.
So, we can take:
Adjacent side (AB) = $4k$
Opposite side (BC) = $3k$
where $k$ is a positive constant.
Using the Pythagoras theorem in $\triangle$ABC:
$AC^2 = AB^2 + BC^2$
(Pythagoras theorem)
$AC^2 = (4k)^2 + (3k)^2$
$AC^2 = 16k^2 + 9k^2$
$AC^2 = 25k^2$
$AC = \sqrt{25k^2}$
$AC = 5k$ (Since length must be positive)
Now, we have the lengths of all three sides in terms of $k$:
Opposite side (BC) = $3k$
Adjacent side (AB) = $4k$
Hypotenuse (AC) = $5k$
Now we calculate $\sin A$, $\cos A$, and $\tan A$:
$\sin A = \frac{\text{Opposite side}}{\text{Hypotenuse}} = \frac{BC}{AC} = \frac{3k}{5k} = \frac{3}{5}$
$\cos A = \frac{\text{Adjacent side}}{\text{Hypotenuse}} = \frac{AB}{AC} = \frac{4k}{5k} = \frac{4}{5}$
$\tan A = \frac{\text{Opposite side}}{\text{Adjacent side}} = \frac{BC}{AB} = \frac{3k}{4k} = \frac{3}{4}$
Now, we calculate the squares of these ratios:
$\sin^2 A = \left(\frac{3}{5}\right)^2 = \frac{9}{25}$
$\cos^2 A = \left(\frac{4}{5}\right)^2 = \frac{16}{25}$
$\tan^2 A = \left(\frac{3}{4}\right)^2 = \frac{9}{16}$
Now, we evaluate the Left Hand Side (LHS) of the given equation:
LHS = $\frac{1\;-\;\tan^{2}A}{1\;+\;\tan^{2}A}$
LHS = $\frac{1 - \frac{9}{16}}{1 + \frac{9}{16}}$
LHS = $\frac{\frac{16}{16} - \frac{9}{16}}{\frac{16}{16} + \frac{9}{16}}$
LHS = $\frac{\frac{16-9}{16}}{\frac{16+9}{16}}$
LHS = $\frac{\frac{7}{16}}{\frac{25}{16}}$
LHS = $\frac{7}{16} \times \frac{16}{25}$
LHS = $\frac{7}{25}$
Now, we evaluate the Right Hand Side (RHS) of the given equation:
RHS = $\cos^2 A - \sin^2 A$
RHS = $\frac{16}{25} - \frac{9}{25}$
RHS = $\frac{16-9}{25}$
RHS = $\frac{7}{25}$
Comparing the LHS and RHS:
LHS = $\frac{7}{25}$
RHS = $\frac{7}{25}$
Since LHS = RHS, the statement is true.
Therefore, $\frac{1\;-\;\tan^{2}A}{1\;+\;\tan^{2}A}$ = $\cos^2 A - \sin^2 A$ is verified.
Question 9. In triangle ABC, right-angled at B, if tan A = $\frac{1}{\sqrt{3}}$ find the value of:
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C
Answer:
Given:
In $\triangle$ABC, right-angled at B,
$\tan A = \frac{1}{\sqrt{3}}$
To Find:
(i) $\sin A \cos C + \cos A \sin C$
(ii) $\cos A \cos C – \sin A \sin C$
Solution:
We are given $\tan A = \frac{1}{\sqrt{3}}$.
In a right-angled triangle ABC, right-angled at B,
$\tan A = \frac{\text{Opposite side to A}}{\text{Adjacent side to A}} = \frac{BC}{AB}$
So, $\frac{BC}{AB} = \frac{1}{\sqrt{3}}$
Let $BC = k$ and $AB = k\sqrt{3}$, where $k$ is a positive constant.
Using the Pythagoras theorem in $\triangle$ABC:
$AC^2 = AB^2 + BC^2$
(Pythagoras theorem)
$AC^2 = (k\sqrt{3})^2 + k^2$
$AC^2 = 3k^2 + k^2$
$AC^2 = 4k^2$
$AC = \sqrt{4k^2} = 2k$ (Since length must be positive)
Now, we find the trigonometric ratios for angles A and C.
For angle A:
Opposite side (BC) = $k$
Adjacent side (AB) = $k\sqrt{3}$
Hypotenuse (AC) = $2k$
$\sin A = \frac{\text{Opposite side}}{\text{Hypotenuse}} = \frac{BC}{AC} = \frac{k}{2k} = \frac{1}{2}$
$\cos A = \frac{\text{Adjacent side}}{\text{Hypotenuse}} = \frac{AB}{AC} = \frac{k\sqrt{3}}{2k} = \frac{\sqrt{3}}{2}$
For angle C:
Opposite side (AB) = $k\sqrt{3}$
Adjacent side (BC) = $k$
Hypotenuse (AC) = $2k$
$\sin C = \frac{\text{Opposite side}}{\text{Hypotenuse}} = \frac{AB}{AC} = \frac{k\sqrt{3}}{2k} = \frac{\sqrt{3}}{2}$
$\cos C = \frac{\text{Adjacent side}}{\text{Hypotenuse}} = \frac{BC}{AC} = \frac{k}{2k} = \frac{1}{2}$
(i) Evaluate $\sin A \cos C + \cos A \sin C$
Substitute the calculated values:
$\sin A \cos C + \cos A \sin C = \left(\frac{1}{2}\right) \times \left(\frac{1}{2}\right) + \left(\frac{\sqrt{3}}{2}\right) \times \left(\frac{\sqrt{3}}{2}\right)$
$= \frac{1}{4} + \frac{\sqrt{3} \times \sqrt{3}}{2 \times 2}$
$= \frac{1}{4} + \frac{3}{4}$
$= \frac{1+3}{4}$
$= \frac{4}{4}$
$= 1$
Note: This is the expansion of $\sin(A+C)$. Since $\angle B = 90^\circ$, $\angle A + \angle C = 90^\circ$, so $\sin(A+C) = \sin(90^\circ) = 1$. This confirms our calculation.
(ii) Evaluate $\cos A \cos C – \sin A \sin C$
Substitute the calculated values:
$\cos A \cos C – \sin A \sin C = \left(\frac{\sqrt{3}}{2}\right) \times \left(\frac{1}{2}\right) - \left(\frac{1}{2}\right) \times \left(\frac{\sqrt{3}}{2}\right)$
$= \frac{\sqrt{3}}{4} - \frac{\sqrt{3}}{4}$
$= 0$
Note: This is the expansion of $\cos(A+C)$. Since $\angle A + \angle C = 90^\circ$, $\cos(A+C) = \cos(90^\circ) = 0$. This confirms our calculation.
Question 10. In ∆ PQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.
Answer:
Given:
In $\triangle$PQR, right-angled at Q,
PQ = 5 cm
PR + QR = 25 cm
To Find:
$\sin P$, $\cos P$, and $\tan P$
Solution:
In right-angled $\triangle$PQR, by Pythagoras theorem, we have:
$PQ^2 + QR^2 = PR^2$
(Pythagoras theorem)
We are given $PR + QR = 25$ cm. Let $QR = x$. Then $PR = 25 - x$.
Substitute these values into the Pythagoras theorem equation:
$(5)^2 + x^2 = (25 - x)^2$
$25 + x^2 = 25^2 - 2(25)x + x^2$
$25 + x^2 = 625 - 50x + x^2$
Subtract $x^2$ from both sides of the equation:
$25 = 625 - 50x$
Rearrange the terms to solve for $x$:
$50x = 625 - 25$
$50x = 600$
$x = \frac{600}{50}$
$x = 12$
So, $QR = 12$ cm.
Now, find the length of PR:
$PR = 25 - QR = 25 - 12 = 13$ cm.
The side lengths of $\triangle$PQR are:
PQ = 5 cm
QR = 12 cm
PR = 13 cm
Now, we determine the trigonometric ratios for angle P. For angle P in $\triangle$PQR:
Opposite side to angle P = QR = 12 cm
Adjacent side to angle P = PQ = 5 cm
Hypotenuse = PR = 13 cm
$\sin P = \frac{\text{Opposite side}}{\text{Hypotenuse}} = \frac{QR}{PR} = \frac{12}{13}$
$\cos P = \frac{\text{Adjacent side}}{\text{Hypotenuse}} = \frac{PQ}{PR} = \frac{5}{13}$
$\tan P = \frac{\text{Opposite side}}{\text{Adjacent side}} = \frac{QR}{PQ} = \frac{12}{5}$
Thus, the values are $\sin P = \frac{12}{13}$, $\cos P = \frac{5}{13}$, and $\tan P = \frac{12}{5}$.
Question 11. State whether the following are true or false. Justify your answer.
(i) The value of tan A is always less than 1.
(ii) sec A = $\frac{12}{5}$ for some value of angle A.
(iii) cos A is the abbreviation used for the cosecant of angle A.
(iv) cot A is the product of cot and A.
(v) sin θ = $\frac{4}{3}$ for some angle θ.
Answer:
(i) The value of tan A is always less than 1.
False
Justification: In a right-angled triangle, $\tan A = \frac{\text{Opposite side}}{\text{Adjacent side}}$. The ratio of the opposite side to the adjacent side can be less than, equal to, or greater than 1. For example, if the opposite side is greater than the adjacent side, then $\tan A > 1$. Consider a right triangle with sides 3, 4, and 5 (hypotenuse). If A is the angle opposite the side of length 4 and adjacent to the side of length 3, then $\tan A = \frac{4}{3} > 1$. The value of $\tan A$ is less than 1 only when the side opposite to angle A is shorter than the side adjacent to angle A.
(ii) sec A = $\frac{12}{5}$ for some value of angle A.
True
Justification: In a right-angled triangle, $\sec A = \frac{\text{Hypotenuse}}{\text{Adjacent side}}$. The hypotenuse is always the longest side in a right triangle. Therefore, Hypotenuse > Adjacent side, which means $\frac{\text{Hypotenuse}}{\text{Adjacent side}} > 1$. The given value $\frac{12}{5} = 2.4$, which is greater than 1. It is possible to construct a right triangle where the hypotenuse is 12 units and the adjacent side is 5 units (the opposite side would be $\sqrt{12^2 - 5^2} = \sqrt{144 - 25} = \sqrt{119}$ units). So, $\sec A = \frac{12}{5}$ is possible for some angle A.
(iii) cos A is the abbreviation used for the cosecant of angle A.
False
Justification: The abbreviation 'cos A' stands for the cosine of angle A. The abbreviation used for the cosecant of angle A is 'cosec A' or 'csc A'.
(iv) cot A is the product of cot and A.
False
Justification: 'cot A' is a single term representing the cotangent of the angle A. The 'cot' part is the name of the trigonometric ratio (cotangent), and 'A' is the argument (the angle). It does not mean 'cot' multiplied by 'A'. The expression 'cot' alone has no meaning without an angle.
(v) sin θ = $\frac{4}{3}$ for some angle θ.
False
Justification: In a right-angled triangle, $\sin \theta = \frac{\text{Opposite side}}{\text{Hypotenuse}}$. The opposite side in a right triangle is always less than or equal to the hypotenuse (equality holds for $\theta = 90^\circ$, which is not acute, but even then the ratio is 1). Therefore, the value of $\sin \theta$ must be less than or equal to 1. The given value $\frac{4}{3} \approx 1.33$, which is greater than 1. Hence, $\sin \theta = \frac{4}{3}$ is not possible for any angle $\theta$.
Example 6 to 8 (Before Exercise 8.2)
Example 6. In ∆ ABC, right-angled at B, AB = 5 cm and ∠ACB = 30° (see Fig. 8.19). Determine the lengths of the sides BC and AC.

Answer:
Given:
In $\triangle$ABC, right-angled at B,
AB = 5 cm
$\angle$ACB = 30$^\circ$
To Find:
Lengths of sides BC and AC.
Solution:
In the right-angled triangle $\triangle$ABC, we are given the side AB and the angle $\angle$C = 30$^\circ$.
With respect to angle C = 30$^\circ$, AB is the opposite side and BC is the adjacent side. AC is the hypotenuse.
We can use the trigonometric ratio $\tan$ to find the length of BC:
$\tan C = \frac{\text{Opposite side}}{\text{Adjacent side}}$
$\tan 30^\circ = \frac{AB}{BC}$
We know that $\tan 30^\circ = \frac{1}{\sqrt{3}}$.
So, $\frac{1}{\sqrt{3}} = \frac{5}{BC}$
To find BC, cross-multiply:
$BC \times 1 = 5 \times \sqrt{3}$
$BC = 5\sqrt{3}$ cm
Now, we can use the trigonometric ratio $\sin$ to find the length of AC:
$\sin C = \frac{\text{Opposite side}}{\text{Hypotenuse}}$
$\sin 30^\circ = \frac{AB}{AC}$
We know that $\sin 30^\circ = \frac{1}{2}$.
So, $\frac{1}{2} = \frac{5}{AC}$
To find AC, cross-multiply:
$AC \times 1 = 5 \times 2$
$AC = 10$ cm
Alternatively, after finding BC, we could use the Pythagoras theorem to find AC:
$AC^2 = AB^2 + BC^2$
(Pythagoras theorem)
$AC^2 = (5)^2 + (5\sqrt{3})^2$
$AC^2 = 25 + (25 \times 3)$
$AC^2 = 25 + 75$
$AC^2 = 100$
$AC = \sqrt{100}$
$AC = 10$ cm (Since length must be positive)
Thus, the lengths of the sides are BC = $5\sqrt{3}$ cm and AC = 10 cm.
Example 7. In ∆ PQR, right-angled at Q (see Fig. 8.20), PQ = 3 cm and PR = 6 cm. Determine ∠QPR and ∠PRQ.
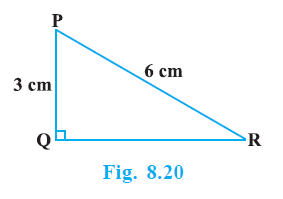
Answer:
Given:
In $\triangle$PQR, right-angled at Q,
PQ = 3 cm
PR = 6 cm
To Find:
$\angle$QPR (or $\angle$P) and $\angle$PRQ (or $\angle$R).
Solution:
In the right-angled triangle $\triangle$PQR, we are given the side PQ and the hypotenuse PR.
Consider angle R ($\angle$PRQ). The side opposite to angle R is PQ, and the hypotenuse is PR.
Using the sine ratio for angle R:
$\sin R = \frac{\text{Opposite side}}{\text{Hypotenuse}} = \frac{PQ}{PR}$
Substitute the given values:
$\sin R = \frac{3}{6} = \frac{1}{2}$
We know that $\sin 30^\circ = \frac{1}{2}$.
Therefore,
$\angle R = 30^\circ$
So, $\angle$PRQ = 30$^\circ$.
Now, consider angle P ($\angle$QPR). We can use the angle sum property of a triangle. In $\triangle$PQR, the sum of angles is 180$^\circ$.
$\angle P + \angle Q + \angle R = 180^\circ$
Substitute the known values ($\angle Q = 90^\circ$ and $\angle R = 30^\circ$):
$\angle P + 90^\circ + 30^\circ = 180^\circ$
$\angle P + 120^\circ = 180^\circ$
$\angle P = 180^\circ - 120^\circ$
$\angle P = 60^\circ$
So, $\angle$QPR = 60$^\circ$.
Alternatively, we could find angle P directly using a trigonometric ratio. With respect to angle P, PQ is the adjacent side and PR is the hypotenuse.
Using the cosine ratio for angle P:
$\cos P = \frac{\text{Adjacent side}}{\text{Hypotenuse}} = \frac{PQ}{PR}$
Substitute the given values:
$\cos P = \frac{3}{6} = \frac{1}{2}$
We know that $\cos 60^\circ = \frac{1}{2}$.
Therefore,
$\angle P = 60^\circ$
So, $\angle$QPR = 60$^\circ$.
Then, using the angle sum property:
$\angle R = 180^\circ - 90^\circ - 60^\circ = 30^\circ$
So, $\angle$PRQ = 30$^\circ$.
The values of the angles are $\angle$QPR = 60$^\circ$ and $\angle$PRQ = 30$^\circ$.
Example 8. If sin (A – B) = $\frac{1}{2}$ , cos (A + B) = $\frac{1}{2}$ , 0° < A + B ≤ 90°, A > B, find A and B.
Answer:
Given:
$\sin (A - B) = \frac{1}{2}$
$\cos (A + B) = \frac{1}{2}$
$0^\circ < A + B \leq 90^\circ$, $A > B$
To Find:
Values of A and B.
Solution:
We are given the equations:
$\sin (A - B) = \frac{1}{2}$
... (i)
$\cos (A + B) = \frac{1}{2}$
... (ii)
We know that $\sin 30^\circ = \frac{1}{2}$. From equation (i), we have:
$\sin (A - B) = \sin 30^\circ$
Since $0^\circ < A + B \leq 90^\circ$ and $A > B$, $(A-B)$ must be in the range $(0^\circ, 90^\circ)$. In this range, the sine function is one-to-one, so we can equate the arguments:
$A - B = 30^\circ$
... (iii)
We also know that $\cos 60^\circ = \frac{1}{2}$. From equation (ii), we have:
$\cos (A + B) = \cos 60^\circ$
Given that $0^\circ < A + B \leq 90^\circ$. In this range, the cosine function is one-to-one, so we can equate the arguments:
$A + B = 60^\circ$
... (iv)
Now we solve the system of linear equations (iii) and (iv):
$A - B = 30^\circ$
$A + B = 60^\circ$
Adding equation (iii) and equation (iv):
$(A - B) + (A + B) = 30^\circ + 60^\circ$
$2A = 90^\circ$
$A = \frac{90^\circ}{2}$
$A = 45^\circ$
Substitute the value of A into equation (iv):
$45^\circ + B = 60^\circ$
$B = 60^\circ - 45^\circ$
$B = 15^\circ$
We verify if these values satisfy the given conditions: $A = 45^\circ$, $B = 15^\circ$.
$A > B$: $45^\circ > 15^\circ$ (True)
$0^\circ < A + B \leq 90^\circ$: $A + B = 45^\circ + 15^\circ = 60^\circ$. $0^\circ < 60^\circ \leq 90^\circ$ (True)
Thus, the values of A and B are $45^\circ$ and $15^\circ$ respectively.
Exercise 8.2
Question 1. Evaluate the following :
(i) sin 60° cos 30° + sin 30° cos 60°
(ii) 2 tan2 45° + cos2 30° – sin2 60°
(iii) $\frac{cos \;45°}{ sec \;30° \;+\; cosec \;30°}$
(iv) $\frac{ sin \;30° \;+\; tan \;45° \;-\; cosec \;60°}{ sec \;30° \;+\; cos\; 60° \;+\; cot\; 45°}$
(v) $\frac{5 \ cos^2 \;60° \;+\; 4 \ sec^2 \;30° \;-\; tan^2 \;45°}{sin^2 \;30° \;+\; cos^2 \;30°}$
Answer:
We use the standard trigonometric values for the given angles:
$\sin 30^\circ = \frac{1}{2}$, $\cos 30^\circ = \frac{\sqrt{3}}{2}$, $\tan 30^\circ = \frac{1}{\sqrt{3}}$
$\sin 45^\circ = \frac{1}{\sqrt{2}}$, $\cos 45^\circ = \frac{1}{\sqrt{2}}$, $\tan 45^\circ = 1$
$\sin 60^\circ = \frac{\sqrt{3}}{2}$, $\cos 60^\circ = \frac{1}{2}$, $\tan 60^\circ = \sqrt{3}$
$\text{cosec } \theta = \frac{1}{\sin \theta}$
$\sec \theta = \frac{1}{\cos \theta}$
$\cot \theta = \frac{1}{\tan \theta}$
So,
$\sec 30^\circ = \frac{1}{\cos 30^\circ} = \frac{1}{\sqrt{3}/2} = \frac{2}{\sqrt{3}}$
$\text{cosec } 30^\circ = \frac{1}{\sin 30^\circ} = \frac{1}{1/2} = 2$
$\text{cosec } 60^\circ = \frac{1}{\sin 60^\circ} = \frac{1}{\sqrt{3}/2} = \frac{2}{\sqrt{3}}$
$\cot 45^\circ = \frac{1}{\tan 45^\circ} = \frac{1}{1} = 1$
(i) Evaluate $\sin 60^\circ \cos 30^\circ + \sin 30^\circ \cos 60^\circ$
$\sin 60^\circ \cos 30^\circ + \sin 30^\circ \cos 60^\circ = \left(\frac{\sqrt{3}}{2}\right) \left(\frac{\sqrt{3}}{2}\right) + \left(\frac{1}{2}\right) \left(\frac{1}{2}\right)$
$= \frac{(\sqrt{3})^2}{2^2} + \frac{1^2}{2^2}$
$= \frac{3}{4} + \frac{1}{4}$
$= \frac{3+1}{4}$
$= \frac{4}{4}$
$= 1$
(ii) Evaluate $2 \tan^2 45^\circ + \cos^2 30^\circ – \sin^2 60^\circ$
$2 \tan^2 45^\circ + \cos^2 30^\circ – \sin^2 60^\circ = 2 (1)^2 + \left(\frac{\sqrt{3}}{2}\right)^2 - \left(\frac{\sqrt{3}}{2}\right)^2$
$= 2(1) + \frac{3}{4} - \frac{3}{4}$
$= 2 + 0$
$= 2$
(iii) Evaluate $\frac{\cos \;45°}{ \sec \;30° \;+\; \text{cosec} \;30°}$
$\frac{\cos \;45°}{ \sec \;30° \;+\; \text{cosec} \;30°} = \frac{\frac{1}{\sqrt{2}}}{\frac{2}{\sqrt{3}} + 2}$
$= \frac{\frac{1}{\sqrt{2}}}{\frac{2 + 2\sqrt{3}}{\sqrt{3}}}$
$= \frac{1}{\sqrt{2}} \times \frac{\sqrt{3}}{2 + 2\sqrt{3}}$
$= \frac{\sqrt{3}}{2\sqrt{2} + 2\sqrt{6}}$
Rationalize the denominator:
$= \frac{\sqrt{3}}{2(\sqrt{2} + \sqrt{6})} \times \frac{\sqrt{6} - \sqrt{2}}{\sqrt{6} - \sqrt{2}}$
$= \frac{\sqrt{3}(\sqrt{6} - \sqrt{2})}{2((\sqrt{6})^2 - (\sqrt{2})^2)}$
$= \frac{\sqrt{18} - \sqrt{6}}{2(6 - 2)}$
$= \frac{\sqrt{9 \times 2} - \sqrt{6}}{2(4)}$
$= \frac{3\sqrt{2} - \sqrt{6}}{8}$
(iv) Evaluate $\frac{ \sin \;30° \;+\; \tan \;45° \;-\; \text{cosec} \;60°}{ \sec \;30° \;+\; \cos\; 60° \;+\; \cot\; 45°}$
Substitute the values:
Numerator = $\sin 30^\circ + \tan 45^\circ - \text{cosec } 60^\circ = \frac{1}{2} + 1 - \frac{2}{\sqrt{3}}$
$= \frac{1}{2} + \frac{2}{2} - \frac{2}{\sqrt{3}} = \frac{3}{2} - \frac{2}{\sqrt{3}} = \frac{3\sqrt{3} - 4}{2\sqrt{3}}$
Denominator = $\sec 30^\circ + \cos 60^\circ + \cot 45^\circ = \frac{2}{\sqrt{3}} + \frac{1}{2} + 1$
$= \frac{2}{\sqrt{3}} + \frac{1}{2} + \frac{2}{2} = \frac{2}{\sqrt{3}} + \frac{3}{2} = \frac{4 + 3\sqrt{3}}{2\sqrt{3}}$
Now, divide the numerator by the denominator:
$\frac{\frac{3\sqrt{3} - 4}{2\sqrt{3}}}{\frac{4 + 3\sqrt{3}}{2\sqrt{3}}} = \frac{3\sqrt{3} - 4}{2\sqrt{3}} \times \frac{2\sqrt{3}}{3\sqrt{3} + 4}$
$= \frac{3\sqrt{3} - 4}{3\sqrt{3} + 4}$
Rationalize the denominator:
$= \frac{(3\sqrt{3} - 4)}{(3\sqrt{3} + 4)} \times \frac{(3\sqrt{3} - 4)}{(3\sqrt{3} - 4)}$
$= \frac{(3\sqrt{3})^2 - 2(3\sqrt{3})(4) + 4^2}{(3\sqrt{3})^2 - 4^2}$
$= \frac{27 - 24\sqrt{3} + 16}{27 - 16}$
$= \frac{43 - 24\sqrt{3}}{11}$
(v) Evaluate $\frac{5 \cos^2 \;60° \;+\; 4 \sec^2 \;30° \;-\; \tan^2 \;45°}{\sin^2 \;30° \;+\; \cos^2 \;30°}$
Substitute the values:
Numerator = $5 \left(\frac{1}{2}\right)^2 + 4 \left(\frac{2}{\sqrt{3}}\right)^2 - (1)^2$
$= 5 \left(\frac{1}{4}\right) + 4 \left(\frac{4}{3}\right) - 1$
$= \frac{5}{4} + \frac{16}{3} - 1$
Find a common denominator (12):
$= \frac{5 \times 3}{4 \times 3} + \frac{16 \times 4}{3 \times 4} - \frac{1 \times 12}{1 \times 12}$
$= \frac{15}{12} + \frac{64}{12} - \frac{12}{12}$
$= \frac{15 + 64 - 12}{12} = \frac{79 - 12}{12} = \frac{67}{12}$
Denominator = $\sin^2 30^\circ + \cos^2 30^\circ = \left(\frac{1}{2}\right)^2 + \left(\frac{\sqrt{3}}{2}\right)^2$
$= \frac{1}{4} + \frac{3}{4} = \frac{1+3}{4} = \frac{4}{4} = 1$
Alternatively, using the identity $\sin^2 \theta + \cos^2 \theta = 1$, the denominator is $\sin^2 30^\circ + \cos^2 30^\circ = 1$.
Now, divide the numerator by the denominator:
$\frac{\frac{67}{12}}{1} = \frac{67}{12}$
Question 2. Choose the correct option and justify your choice :
(i) $\frac{2 \ tan\; 30°}{1 \;+\; tan^{2}\;30°}$ =
(A) sin 60°
(B) cos 60°
(C) tan 60°
(D) sin 30°
(ii) $\frac{1 \;-\; tan^{2}\;45°}{1 \;+\; tan^{2}\;45°}$ =
(A) tan 90°
(B) 1
(C) sin 45°
(D) 0
(iii) sin 2A = 2 sin A is true when A =
(A) 0°
(B) 30°
(C) 45°
(D) 60°
(iv) $\frac{2 \ tan \;30° }{1 \;-\; tan^{2}\;30° }$ =
(A) cos 60°
(B) sin 60°
(C) tan 60°
(D) sin 30°
Answer:
(i) $\frac{2 \tan\; 30°}{1 \;+\; \tan^{2}\;30°}$
We know that $\tan 30^\circ = \frac{1}{\sqrt{3}}$.
Substitute this value into the expression:
$\frac{2 \tan 30^\circ}{1 + \tan^2 30^\circ} = \frac{2 \times \frac{1}{\sqrt{3}}}{1 + \left(\frac{1}{\sqrt{3}}\right)^2}$
$= \frac{\frac{2}{\sqrt{3}}}{1 + \frac{1}{3}}$
$= \frac{\frac{2}{\sqrt{3}}}{\frac{3+1}{3}}$
$= \frac{\frac{2}{\sqrt{3}}}{\frac{4}{3}}$
$= \frac{2}{\sqrt{3}} \times \frac{3}{4}$
$= \frac{6}{4\sqrt{3}}$
$= \frac{3}{2\sqrt{3}}$
Rationalize the denominator:
$= \frac{3}{2\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}$
$= \frac{3\sqrt{3}}{2 \times 3}$
$= \frac{\sqrt{3}}{2}$
Comparing this value with the options:
(A) $\sin 60^\circ = \frac{\sqrt{3}}{2}$
(B) $\cos 60^\circ = \frac{1}{2}$
(C) $\tan 60^\circ = \sqrt{3}$
(D) $\sin 30^\circ = \frac{1}{2}$
The value of the expression is equal to $\sin 60^\circ$.
Correct option is (A).
(ii) $\frac{1 \;-\; \tan^{2}\;45°}{1 \;+\; \tan^{2}\;45°}$
We know that $\tan 45^\circ = 1$.
Substitute this value into the expression:
$\frac{1 - \tan^2 45^\circ}{1 + \tan^2 45^\circ} = \frac{1 - (1)^2}{1 + (1)^2}$
$= \frac{1 - 1}{1 + 1}$
$= \frac{0}{2}$
$= 0$
Comparing this value with the options:
(A) $\tan 90^\circ$ is undefined.
(B) $1$
(C) $\sin 45^\circ = \frac{1}{\sqrt{2}}$
(D) $0$
The value of the expression is equal to 0.
Correct option is (D).
(iii) $\sin 2A = 2 \sin A$ is true when A =
We check each option:
(A) A = 0°
LHS = $\sin (2 \times 0^\circ) = \sin 0^\circ = 0$
RHS = $2 \sin 0^\circ = 2 \times 0 = 0$
Since LHS = RHS ($0 = 0$), the statement is true for A = 0°.
(B) A = 30°
LHS = $\sin (2 \times 30^\circ) = \sin 60^\circ = \frac{\sqrt{3}}{2}$
RHS = $2 \sin 30^\circ = 2 \times \frac{1}{2} = 1$
LHS $\neq$ RHS.
(C) A = 45°
LHS = $\sin (2 \times 45^\circ) = \sin 90^\circ = 1$
RHS = $2 \sin 45^\circ = 2 \times \frac{1}{\sqrt{2}} = \sqrt{2}$
LHS $\neq$ RHS.
(D) A = 60°
LHS = $\sin (2 \times 60^\circ) = \sin 120^\circ = \sin (180^\circ - 60^\circ) = \sin 60^\circ = \frac{\sqrt{3}}{2}$
RHS = $2 \sin 60^\circ = 2 \times \frac{\sqrt{3}}{2} = \sqrt{3}$
LHS $\neq$ RHS.
The statement is true only for A = 0° among the given options.
Correct option is (A).
(iv) $\frac{2 \tan \;30° }{1 \;-\; \tan^{2}\;30° }$
We know that $\tan 30^\circ = \frac{1}{\sqrt{3}}$.
Substitute this value into the expression:
$\frac{2 \tan 30^\circ}{1 - \tan^2 30^\circ} = \frac{2 \times \frac{1}{\sqrt{3}}}{1 - \left(\frac{1}{\sqrt{3}}\right)^2}$
$= \frac{\frac{2}{\sqrt{3}}}{1 - \frac{1}{3}}$
$= \frac{\frac{2}{\sqrt{3}}}{\frac{3-1}{3}}$
$= \frac{\frac{2}{\sqrt{3}}}{\frac{2}{3}}$
$= \frac{2}{\sqrt{3}} \times \frac{3}{2}$
$= \frac{3}{\sqrt{3}}$
Rationalize the denominator:
$= \frac{3}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}$
$= \frac{3\sqrt{3}}{3}$
$= \sqrt{3}$
Comparing this value with the options:
(A) $\cos 60^\circ = \frac{1}{2}$
(B) $\sin 60^\circ = \frac{\sqrt{3}}{2}$
(C) $\tan 60^\circ = \sqrt{3}$
(D) $\sin 30^\circ = \frac{1}{2}$
The value of the expression is equal to $\tan 60^\circ$.
Correct option is (C).
Question 3. If tan (A + B) = $\sqrt{3}$ and tan (A – B) = $\frac{1}{\sqrt{3}}$ ; 0° < A + B ≤ 90°; A > B, find A and B.
Answer:
Given:
$\tan (A + B) = \sqrt{3}$
$\tan (A - B) = \frac{1}{\sqrt{3}}$
$0^\circ < A + B \leq 90^\circ$, $A > B$
To Find:
Values of A and B.
Solution:
We are given the equations:
$\tan (A + B) = \sqrt{3}$
$\tan (A - B) = \frac{1}{\sqrt{3}}$
We know that $\tan 60^\circ = \sqrt{3}$. From the first equation, since $0^\circ < A + B \leq 90^\circ$, we can write:
$\tan (A + B) = \tan 60^\circ$
Equating the arguments (since A+B is in the domain where tan is invertible):
$A + B = 60^\circ$
... (i)
We know that $\tan 30^\circ = \frac{1}{\sqrt{3}}$. From the second equation, since A > B and $A+B \leq 90^\circ$, $(A-B)$ must be positive and acute, so we can write:
$\tan (A - B) = \tan 30^\circ$
Equating the arguments:
$A - B = 30^\circ$
... (ii)
Now we have a system of two linear equations with variables A and B:
$A + B = 60^\circ$
$A - B = 30^\circ$
Adding equation (i) and equation (ii):
$(A + B) + (A - B) = 60^\circ + 30^\circ$
$2A = 90^\circ$
$A = \frac{90^\circ}{2}$
$A = 45^\circ$
Substitute the value of A into equation (i):
$45^\circ + B = 60^\circ$
$B = 60^\circ - 45^\circ$
$B = 15^\circ$
We check the given conditions with the found values $A = 45^\circ$ and $B = 15^\circ$:
$A > B$: $45^\circ > 15^\circ$ (True)
$0^\circ < A + B \leq 90^\circ$: $A + B = 45^\circ + 15^\circ = 60^\circ$. $0^\circ < 60^\circ \leq 90^\circ$ (True)
The values satisfy all conditions.
Thus, the values of A and B are $45^\circ$ and $15^\circ$ respectively.
Question 4. State whether the following are true or false. Justify your answer.
(i) sin (A + B) = sin A + sin B.
(ii) The value of sin θ increases as θ increases.
(iii) The value of cos θ increases as θ increases.
(iv) sin θ = cos θ for all values of θ.
(v) cot A is not defined for A = 0°.
Answer:
(i) sin (A + B) = sin A + sin B.
False
Justification: This statement is not true in general. The correct identity for $\sin(A+B)$ is $\sin(A+B) = \sin A \cos B + \cos A \sin B$. We can demonstrate this with a counterexample. Let $A = 30^\circ$ and $B = 60^\circ$.
LHS = $\sin (A + B) = \sin (30^\circ + 60^\circ) = \sin 90^\circ = 1$
RHS = $\sin A + \sin B = \sin 30^\circ + \sin 60^\circ = \frac{1}{2} + \frac{\sqrt{3}}{2} = \frac{1 + \sqrt{3}}{2}$
Since $1 \neq \frac{1 + \sqrt{3}}{2}$, the statement $\sin(A+B) = \sin A + \sin B$ is false.
(ii) The value of sin θ increases as θ increases.
True
Justification: For $0^\circ \leq \theta \leq 90^\circ$, as the angle $\theta$ increases, the value of $\sin \theta$ also increases. We can see this from the standard values:
$\sin 0^\circ = 0$
$\sin 30^\circ = 0.5$
$\sin 45^\circ = \frac{1}{\sqrt{2}} \approx 0.707$
$\sin 60^\circ = \frac{\sqrt{3}}{2} \approx 0.866$
$\sin 90^\circ = 1$
The values clearly increase from 0 to 1 as $\theta$ increases from 0° to 90°.
(iii) The value of cos θ increases as θ increases.
False
Justification: For $0^\circ \leq \theta \leq 90^\circ$, as the angle $\theta$ increases, the value of $\cos \theta$ decreases. We can see this from the standard values:
$\cos 0^\circ = 1$
$\cos 30^\circ = \frac{\sqrt{3}}{2} \approx 0.866$
$\cos 45^\circ = \frac{1}{\sqrt{2}} \approx 0.707$
$\cos 60^\circ = 0.5$
$\cos 90^\circ = 0$
The values clearly decrease from 1 to 0 as $\theta$ increases from 0° to 90°.
(iv) sin θ = cos θ for all values of θ.
False
Justification: The values of $\sin \theta$ and $\cos \theta$ are equal only for specific values of $\theta$, such as $\theta = 45^\circ$ (in the first quadrant). For example, if we take $\theta = 30^\circ$, $\sin 30^\circ = \frac{1}{2}$ and $\cos 30^\circ = \frac{\sqrt{3}}{2}$. Since $\frac{1}{2} \neq \frac{\sqrt{3}}{2}$, $\sin \theta \neq \cos \theta$ for $\theta = 30^\circ$. Therefore, the statement is false for all values of $\theta$.
(v) cot A is not defined for A = 0°.
True
Justification: The cotangent of an angle A is defined as $\cot A = \frac{\cos A}{\sin A}$. For $A = 0^\circ$, we have $\cos 0^\circ = 1$ and $\sin 0^\circ = 0$. Thus, $\cot 0^\circ = \frac{\cos 0^\circ}{\sin 0^\circ} = \frac{1}{0}$. Division by zero is undefined. Therefore, $\cot A$ is not defined for $A = 0^\circ$.
Example 9 to 12 (Before Exercise 8.3)
Example 9. Express the ratios cos A, tan A and sec A in terms of sin A.
Answer:
To Express:
$\cos A$, $\tan A$ and $\sec A$ in terms of $\sin A$.
Solution:
We use the fundamental trigonometric identity:
$\sin^2 A + \cos^2 A = 1$
Expressing $\cos A$ in terms of $\sin A$:
From the identity, we have:
$\cos^2 A = 1 - \sin^2 A$
Taking the square root of both sides:
$\cos A = \pm \sqrt{1 - \sin^2 A}$
For an acute angle A, $\cos A$ is positive, so we take the positive root:
$\cos A = \sqrt{1 - \sin^2 A}$
Expressing $\tan A$ in terms of $\sin A$:
We know that $\tan A = \frac{\sin A}{\cos A}$.
Substitute the expression for $\cos A$ in terms of $\sin A$ (assuming A is acute):
$\tan A = \frac{\sin A}{\sqrt{1 - \sin^2 A}}$
Expressing $\sec A$ in terms of $\sin A$:
We know that $\sec A = \frac{1}{\cos A}$.
Substitute the expression for $\cos A$ in terms of $\sin A$ (assuming A is acute):
$\sec A = \frac{1}{\sqrt{1 - \sin^2 A}}$
Example 10. Prove that sec A (1 – sin A)(sec A + tan A) = 1.
Answer:
To Prove:
$\sec A (1 – \sin A)(\sec A + \tan A) = 1$
Proof:
We start with the Left Hand Side (LHS) of the equation and simplify it using trigonometric identities to reach the Right Hand Side (RHS).
LHS = $\sec A (1 – \sin A)(\sec A + \tan A)$
We express $\sec A$ and $\tan A$ in terms of $\sin A$ and $\cos A$:
$\sec A = \frac{1}{\cos A}$
$\tan A = \frac{\sin A}{\cos A}$
Substitute these into the expression:
LHS = $\frac{1}{\cos A} (1 – \sin A) \left(\frac{1}{\cos A} + \frac{\sin A}{\cos A}\right)$
Combine the terms within the second parenthesis:
LHS = $\frac{1}{\cos A} (1 – \sin A) \left(\frac{1 + \sin A}{\cos A}\right)$
Multiply the terms:
LHS = $\frac{(1 – \sin A)(1 + \sin A)}{\cos A \times \cos A}$
Use the algebraic identity $(a-b)(a+b) = a^2 - b^2$ in the numerator:
LHS = $\frac{1^2 – \sin^2 A}{\cos^2 A}$
LHS = $\frac{1 – \sin^2 A}{\cos^2 A}$
Use the fundamental trigonometric identity $1 - \sin^2 A = \cos^2 A$ in the numerator:
LHS = $\frac{\cos^2 A}{\cos^2 A}$
Assuming $\cos A \neq 0$, we can cancel out $\cos^2 A$:
LHS = $1$
This is equal to the Right Hand Side (RHS).
LHS = RHS
Hence, the identity is proved.
Example 11. Prove that $\frac{cot \;A \;-\; cos \;A}{cot \;A \;+\; cos\; A}$ = $\frac{cosec \;A \;-\; 1}{cosec \;A \;+\; 1}$
Answer:
To Prove:
$\frac{\cot \;A \;-\; \cos \;A}{\cot \;A \;+\; \cos\; A} = \frac{\text{cosec} \;A \;-\; 1}{\text{cosec} \;A \;+\; 1}$
Proof:
We start with the Left Hand Side (LHS) of the equation and simplify it to obtain the Right Hand Side (RHS).
LHS = $\frac{\cot \;A \;-\; \cos \;A}{\cot \;A \;+\; \cos\; A}$
Express $\cot A$ in terms of $\sin A$ and $\cos A$:
$\cot A = \frac{\cos A}{\sin A}$
Substitute this into the LHS expression:
LHS = $\frac{\frac{\cos A}{\sin A} \;-\; \cos \;A}{\frac{\cos A}{\sin A} \;+\; \cos\; A}$
Take $\cos A$ common from the numerator and the denominator:
LHS = $\frac{\cos A \left(\frac{1}{\sin A} \;-\; 1\right)}{\cos A \left(\frac{1}{\sin A} \;+\; 1\right)}$
Cancel out $\cos A$ from the numerator and denominator (assuming $\cos A \neq 0$):
LHS = $\frac{\frac{1}{\sin A} \;-\; 1}{\frac{1}{\sin A} \;+\; 1}$
We know that $\text{cosec} A = \frac{1}{\sin A}$. Substitute this into the expression:
LHS = $\frac{\text{cosec} \;A \;-\; 1}{\text{cosec} \;A \;+\; 1}$
This is equal to the Right Hand Side (RHS).
LHS = RHS
Hence, the identity is proved.
Example 12. Prove that $\frac{sin \;θ \;-\; cos \;θ \;+\; 1}{sin \;θ \;+\; cos \;θ \;-\; 1}$ = $\frac{1}{sec \;θ \;-\; tan \;θ}$ , using the identity sec2 θ = 1 + tan2 θ.
Answer:
To Prove:
$\frac{\sin \;θ \;-\; \cos \;θ \;+\; 1}{\sin \;θ \;+\; \cos \;θ \;-\; 1} = \frac{1}{\sec \;θ \;-\; \tan \;θ}$ using the identity $\sec^2 \theta = 1 + \tan^2 \theta$.
Proof:
We start with the Left Hand Side (LHS) and manipulate it. Since the RHS involves $\sec \theta$ and $\tan \theta$, we will divide the numerator and denominator of the LHS by $\cos \theta$ to introduce these terms.
LHS = $\frac{\sin \;θ \;-\; \cos \;θ \;+\; 1}{\sin \;θ \;+\; \cos \;θ \;-\; 1}$
Divide the numerator and denominator by $\cos \theta$ (assuming $\cos \theta \neq 0$):
LHS = $\frac{\frac{\sin \;θ}{\cos \;θ} \;-\; \frac{\cos \;θ}{\cos \;θ} \;+\; \frac{1}{\cos \;θ}}{\frac{\sin \;θ}{\cos \;θ} \;+\; \frac{\cos \;θ}{\cos \;θ} \;-\; \frac{1}{\cos \;θ}}$
Substitute $\tan \theta = \frac{\sin \theta}{\cos \theta}$ and $\sec \theta = \frac{1}{\cos \theta}$:
LHS = $\frac{\tan \;θ \;-\; 1 \;+\; \sec \;θ}{\tan \;θ \;+\; 1 \;-\; \sec \;θ}$
Rearrange the terms in the numerator:
LHS = $\frac{(\tan \;θ \;+\; \sec \;θ) \;-\; 1}{(\tan \;θ \;-\; \sec \;θ) \;+\; 1}$
We are given the identity $\sec^2 \theta = 1 + \tan^2 \theta$. Rearranging this identity, we get $1 = \sec^2 \theta - \tan^2 \theta$.
Use the algebraic identity $a^2 - b^2 = (a-b)(a+b)$ on the term $\sec^2 \theta - \tan^2 \theta$:
$1 = (\sec \theta - \tan \theta)(\sec \theta + \tan \theta)$
Substitute this expression for '1' in the numerator of the LHS:
LHS = $\frac{(\tan \;θ \;+\; \sec \;θ) \;-\; (\sec^2 \;θ \;-\; \tan^2 \;θ)}{(\tan \;θ \;-\; \sec \;θ) \;+\; 1}$
LHS = $\frac{(\tan \;θ \;+\; \sec \;θ) \;-\; (\sec \;θ \;-\; \tan \;θ)(\sec \;θ \;+\; \tan \;θ)}{(\tan \;θ \;-\; \sec \;θ) \;+\; 1}$
Take $(\tan \theta + \sec \theta)$ common from the terms in the numerator:
LHS = $\frac{(\tan \;θ \;+\; \sec \;θ) [1 \;-\; (\sec \;θ \;-\; \tan \;θ)]}{(\tan \;θ \;-\; \sec \;θ) \;+\; 1}$
LHS = $\frac{(\tan \;θ \;+\; \sec \;θ) [1 \;-\; \sec \;θ \;+\; \tan \;θ]}{(\tan \;θ \;-\; \sec \;θ) \;+\; 1}$
Observe that the term in the square brackets in the numerator $[1 \;-\; \sec \;θ \;+\; \tan \;θ]$ is the same as the denominator $(\tan \;θ \;-\; \sec \;θ) \;+\; 1$.
Cancel out the common term (assuming $(\tan \;θ \;-\; \sec \;θ) \;+\; 1 \neq 0$):
LHS = $\tan \;θ \;+\; \sec \;θ$
This expression is equal to $\sec \theta + \tan \theta$. The RHS is $\frac{1}{\sec \;θ \;-\; \tan \;θ}$.
We know that $(\sec \theta - \tan \theta)(\sec \theta + \tan \theta) = 1$.
Dividing both sides by $(\sec \theta - \tan \theta)$ (assuming $\sec \theta - \tan \theta \neq 0$):
$\sec \theta + \tan \theta = \frac{1}{\sec \theta - \tan \theta}$
So, LHS = $\sec \theta + \tan \theta = \frac{1}{\sec \theta - \tan \theta}$ = RHS.
Hence, the identity is proved.
Exercise 8.3
Question 1. Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.
Answer:
To Express:
$\sin A$, $\sec A$ and $\tan A$ in terms of $\cot A$.
Solution:
Expressing $\tan A$ in terms of $\cot A$:
We know the reciprocal identity:
$\tan A = \frac{1}{\cot A}$
Expressing $\sin A$ in terms of $\cot A$:
We use the identity $\text{cosec}^2 A = 1 + \cot^2 A$.
We also know that $\text{cosec} A = \frac{1}{\sin A}$.
So, $\frac{1}{\sin^2 A} = 1 + \cot^2 A$
Taking the reciprocal of both sides:
$\sin^2 A = \frac{1}{1 + \cot^2 A}$
Taking the square root of both sides:
$\sin A = \pm \sqrt{\frac{1}{1 + \cot^2 A}} = \pm \frac{1}{\sqrt{1 + \cot^2 A}}$
For an acute angle A, $\sin A$ is positive, so we take the positive root:
$\sin A = \frac{1}{\sqrt{1 + \cot^2 A}}$
Expressing $\sec A$ in terms of $\cot A$:
We use the identity $\sec^2 A = 1 + \tan^2 A$.
Substitute the expression for $\tan A$ in terms of $\cot A$:
$\sec^2 A = 1 + \left(\frac{1}{\cot A}\right)^2$
$\sec^2 A = 1 + \frac{1}{\cot^2 A}$
Combine the terms on the right side:
$\sec^2 A = \frac{\cot^2 A + 1}{\cot^2 A}$
Taking the square root of both sides:
$\sec A = \pm \sqrt{\frac{\cot^2 A + 1}{\cot^2 A}} = \pm \frac{\sqrt{1 + \cot^2 A}}{\sqrt{\cot^2 A}}$
$\sec A = \pm \frac{\sqrt{1 + \cot^2 A}}{|\cot A|}$
For an acute angle A, $\sec A$ is positive and $\cot A$ is positive, so $|\cot A| = \cot A$.
$\sec A = \frac{\sqrt{1 + \cot^2 A}}{\cot A}$
Question 2. Write all the other trigonometric ratios of ∠ A in terms of sec A.
Answer:
To Express:
$\sin A$, $\cos A$, $\tan A$, $\cot A$, and $\text{cosec } A$ in terms of $\sec A$.
Solution:
Expressing $\cos A$ in terms of $\sec A$:
We know the reciprocal identity:
$\cos A = \frac{1}{\sec A}$
Expressing $\tan A$ in terms of $\sec A$:
We use the identity $\tan^2 A + 1 = \sec^2 A$.
Rearrange the identity to solve for $\tan^2 A$:
$\tan^2 A = \sec^2 A - 1$
Take the square root of both sides:
$\tan A = \pm \sqrt{\sec^2 A - 1}$
For an acute angle A, $\tan A$ is positive, so we take the positive root:
$\tan A = \sqrt{\sec^2 A - 1}$
Expressing $\sin A$ in terms of $\sec A$:
We use the identity $\sin^2 A + \cos^2 A = 1$.
Substitute the expression for $\cos A$ in terms of $\sec A$:
$\sin^2 A + \left(\frac{1}{\sec A}\right)^2 = 1$
$\sin^2 A + \frac{1}{\sec^2 A} = 1$
Rearrange the equation to solve for $\sin^2 A$:
$\sin^2 A = 1 - \frac{1}{\sec^2 A}$
Combine the terms on the right side:
$\sin^2 A = \frac{\sec^2 A - 1}{\sec^2 A}$
Take the square root of both sides:
$\sin A = \pm \sqrt{\frac{\sec^2 A - 1}{\sec^2 A}} = \pm \frac{\sqrt{\sec^2 A - 1}}{\sqrt{\sec^2 A}}$
$\sin A = \pm \frac{\sqrt{\sec^2 A - 1}}{|\sec A|}$
For an acute angle A, $\sin A$ is positive and $\sec A$ is positive, so $|\sec A| = \sec A$.
$\sin A = \frac{\sqrt{\sec^2 A - 1}}{\sec A}$
Expressing $\cot A$ in terms of $\sec A$:
We know the reciprocal identity $\cot A = \frac{1}{\tan A}$.
Substitute the expression for $\tan A$ in terms of $\sec A$ (assuming A is acute):
$\cot A = \frac{1}{\sqrt{\sec^2 A - 1}}$
Expressing $\text{cosec } A$ in terms of $\sec A$:
We know the reciprocal identity $\text{cosec } A = \frac{1}{\sin A}$.
Substitute the expression for $\sin A$ in terms of $\sec A$ (assuming A is acute):
$\text{cosec } A = \frac{1}{\frac{\sqrt{\sec^2 A - 1}}{\sec A}}$
$\text{cosec } A = \frac{\sec A}{\sqrt{\sec^2 A - 1}}$
Question 3. Choose the correct option. Justify your choice.
(i) 9 sec2 A – 9 tan2 A =
(A) 1
(B) 9
(C) 8
(D) 0
(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ) =
(A) 0
(B) 1
(C) 2
(D) –1
(iii) (sec A + tan A) (1 – sin A) =
(A) sec A
(B) sin A
(C) cosec A
(D) cos A
(iv) $\frac{1 \;+\; tan^2 \;A}{1 \;+\; cot^2 \;A}$ =
(A) sec2 A
(B) –1
(C) cot2 A
(D) tan2 A
Answer:
(i) 9 sec2 A – 9 tan2 A
Take 9 common from the expression:
$9 \sec^2 A - 9 \tan^2 A = 9 (\sec^2 A - \tan^2 A)$
We use the trigonometric identity $\sec^2 A = 1 + \tan^2 A$, which can be rearranged to $\sec^2 A - \tan^2 A = 1$.
Substitute this into the expression:
$9 (\sec^2 A - \tan^2 A) = 9 (1) = 9$
Correct option is (B).
(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ)
Express the terms in $\sin \theta$ and $\cos \theta$:
$\tan \theta = \frac{\sin \theta}{\cos \theta}$
$\sec \theta = \frac{1}{\cos \theta}$
$\cot \theta = \frac{\cos \theta}{\sin \theta}$
$\text{cosec } \theta = \frac{1}{\sin \theta}$
Substitute these into the expression:
$(1 + \frac{\sin \theta}{\cos \theta} + \frac{1}{\cos \theta}) (1 + \frac{\cos \theta}{\sin \theta} - \frac{1}{\sin \theta})$
Combine the terms within each parenthesis:
$(\frac{\cos \theta + \sin \theta + 1}{\cos \theta}) (\frac{\sin \theta + \cos \theta - 1}{\sin \theta})$
Multiply the numerators and the denominators:
$\frac{(\cos \theta + \sin \theta + 1)(\sin \theta + \cos \theta - 1)}{\cos \theta \sin \theta}$
Let $X = \cos \theta + \sin \theta$. The numerator is of the form $(X + 1)(X - 1) = X^2 - 1^2$.
Numerator = $(\cos \theta + \sin \theta)^2 - 1$
Expand $(\cos \theta + \sin \theta)^2$ using $(a+b)^2 = a^2 + 2ab + b^2$:
$= \cos^2 \theta + 2 \sin \theta \cos \theta + \sin^2 \theta - 1$
Use the identity $\sin^2 \theta + \cos^2 \theta = 1$:
$= 1 + 2 \sin \theta \cos \theta - 1$
$= 2 \sin \theta \cos \theta$
Now, substitute the numerator back into the main expression:
$\frac{2 \sin \theta \cos \theta}{\cos \theta \sin \theta}$
Cancel out the common term $\sin \theta \cos \theta$ (assuming $\sin \theta \cos \theta \neq 0$):
$= 2$
Correct option is (C).
(iii) (sec A + tan A) (1 – sin A)
Express the terms in $\sin A$ and $\cos A$:
$\sec A = \frac{1}{\cos A}$
$\tan A = \frac{\sin A}{\cos A}$
Substitute these into the expression:
$(\frac{1}{\cos A} + \frac{\sin A}{\cos A}) (1 – \sin A)$
Combine the terms in the first parenthesis:
$\left(\frac{1 + \sin A}{\cos A}\right) (1 – \sin A)$
Multiply the terms:
$\frac{(1 + \sin A)(1 – \sin A)}{\cos A}$
Use the algebraic identity $(a+b)(a-b) = a^2 - b^2$ in the numerator:
$\frac{1^2 – \sin^2 A}{\cos A}$
$\frac{1 – \sin^2 A}{\cos A}$
Use the trigonometric identity $1 - \sin^2 A = \cos^2 A$ in the numerator:
$\frac{\cos^2 A}{\cos A}$
Cancel out $\cos A$ from the numerator and denominator (assuming $\cos A \neq 0$):
$= \cos A$
Correct option is (D).
(iv) $\frac{1 \;+\; \tan^2 \;A}{1 \;+\; \cot^2 \;A}$
We use the trigonometric identities:
$1 + \tan^2 A = \sec^2 A$
$1 + \cot^2 A = \text{cosec}^2 A$
Substitute these into the expression:
$\frac{1 + \tan^2 A}{1 + \cot^2 A} = \frac{\sec^2 A}{\text{cosec}^2 A}$
Express $\sec A$ and $\text{cosec } A$ in terms of $\sin A$ and $\cos A$:
$\sec^2 A = \left(\frac{1}{\cos A}\right)^2 = \frac{1}{\cos^2 A}$
$\text{cosec}^2 A = \left(\frac{1}{\sin A}\right)^2 = \frac{1}{\sin^2 A}$
Substitute these back into the expression:
$\frac{\frac{1}{\cos^2 A}}{\frac{1}{\sin^2 A}} = \frac{1}{\cos^2 A} \times \frac{\sin^2 A}{1}$
$= \frac{\sin^2 A}{\cos^2 A}$
We know that $\frac{\sin A}{\cos A} = \tan A$. So, $\frac{\sin^2 A}{\cos^2 A} = \tan^2 A$.
Alternatively, using $\cot A = \frac{1}{\tan A}$:
$\frac{1 + \tan^2 A}{1 + \cot^2 A} = \frac{1 + \tan^2 A}{1 + (\frac{1}{\tan A})^2}$
$= \frac{1 + \tan^2 A}{1 + \frac{1}{\tan^2 A}}$
$= \frac{1 + \tan^2 A}{\frac{\tan^2 A + 1}{\tan^2 A}}$
$= (1 + \tan^2 A) \times \frac{\tan^2 A}{1 + \tan^2 A}$
Cancel out the common term $(1 + \tan^2 A)$ (assuming $1 + \tan^2 A \neq 0$):
$= \tan^2 A$
Correct option is (D).
Question 4. Prove the following identities, where the angles involved are acute angles for which the expressions are defined.
(i) (cosec θ - cot θ)2 = $\frac{1 \;-\; cos \;θ}{ 1 \;+\; cos \;θ}$
(ii) $\frac{cos \;A}{1 \;+\; sin \;A}$ + $\frac{1 \;+\; sin \;A}{cos \;A}$ = 2 sec A
(iii) $\frac{tan \;θ}{1 \;-\; cot \;θ}$ + $\frac{cot \;θ}{1 \;-\; tan \;θ}$ = 1 + sec θ cosec θ
[Hint: Write the expression in terms of sin θ and cos θ]
(iv) $\frac{1 \;+\; sec \;A}{sec \;A}$ = $\frac{sin^2 \;A}{1 \;-\; cos \;A}$
[Hint: Simplify LHS and RHS separately]
(v) $\frac{cos \;A \;-\; sin \;A \;+\; 1}{cos \;A \;+\; sin \;A \;-\; 1}$ = cosec A + cot A, using the identity cosec2 A = 1 + cot2 A.
(vi) $\sqrt{\frac{1 \;+\; sin \;A}{1 \;-\; sin \;A}}$ = sec A + tan A
(vii) $\frac{sin \;θ \;-\; 2sin^3 \;θ}{2 cos^3 \;θ \;-\; cos \;θ}$ = tan θ
(viii) (sin A + cosec A)2 + (cos A + sec A)2 = 7 + tan2 A + cot2 A
(ix) (cosec A – sin A)(sec A – cos A) = $\frac{1}{tan \;A \;+\; cot \;A}$
[Hint: Simplify LHS and RHS separately]
(x) $\left( \frac{1\;+\;tan^{2}\;A}{1\;+\;cot^{2}\;A} \right)$ = $\left(\frac{1\;-\;tan \;A}{1\;-\;cot \;A} \right)^{2}$ = tan2 A
Answer:
(i)
To Prove: $(\text{cosec } \theta - \cot \theta)^2 = \frac{1 - \cos \theta}{1 + \cos \theta}$
Proof:
LHS = $(\text{cosec } \theta - \cot \theta)^2$
Express in terms of $\sin \theta$ and $\cos \theta$:
$= \left(\frac{1}{\sin \theta} - \frac{\cos \theta}{\sin \theta}\right)^2$
Combine the terms in the parenthesis:
$= \left(\frac{1 - \cos \theta}{\sin \theta}\right)^2$
Square the numerator and the denominator:
$= \frac{(1 - \cos \theta)^2}{\sin^2 \theta}$
Use the identity $\sin^2 \theta = 1 - \cos^2 \theta$ in the denominator:
$= \frac{(1 - \cos \theta)^2}{1 - \cos^2 \theta}$
Factor the denominator using $a^2 - b^2 = (a-b)(a+b)$:
$= \frac{(1 - \cos \theta)(1 - \cos \theta)}{(1 - \cos \theta)(1 + \cos \theta)}$
Cancel out the common term $(1 - \cos \theta)$ (assuming $1 - \cos \theta \neq 0$, i.e., $\cos \theta \neq 1$):
$= \frac{1 - \cos \theta}{1 + \cos \theta}$
This is equal to the RHS.
LHS = RHS
Hence, the identity is proved.
(ii)
To Prove: $\frac{\cos \;A}{1 \;+\; \sin \;A} + \frac{1 \;+\; \sin \;A}{\cos \;A} = 2 \sec A$
Proof:
LHS = $\frac{\cos \;A}{1 \;+\; \sin \;A} + \frac{1 \;+\; \sin \;A}{\cos \;A}$
Find a common denominator, which is $(1 + \sin A)\cos A$:
$= \frac{\cos A \times \cos A + (1 + \sin A) \times (1 + \sin A)}{(1 + \sin A)\cos A}$
$= \frac{\cos^2 A + (1 + \sin A)^2}{(1 + \sin A)\cos A}$
Expand the term $(1 + \sin A)^2$ in the numerator:
$= \frac{\cos^2 A + (1^2 + 2 \times 1 \times \sin A + \sin^2 A)}{(1 + \sin A)\cos A}$
$= \frac{\cos^2 A + 1 + 2 \sin A + \sin^2 A}{(1 + \sin A)\cos A}$
Group $\cos^2 A + \sin^2 A$ and use the identity $\sin^2 A + \cos^2 A = 1$:
$= \frac{(\cos^2 A + \sin^2 A) + 1 + 2 \sin A}{(1 + \sin A)\cos A}$
$= \frac{1 + 1 + 2 \sin A}{(1 + \sin A)\cos A}$
$= \frac{2 + 2 \sin A}{(1 + \sin A)\cos A}$
Factor out 2 from the numerator:
$= \frac{2(1 + \sin A)}{(1 + \sin A)\cos A}$
Cancel out the common term $(1 + \sin A)$ (assuming $1 + \sin A \neq 0$):
$= \frac{2}{\cos A}$
Use the reciprocal identity $\frac{1}{\cos A} = \sec A$:
$= 2 \sec A$
This is equal to the RHS.
LHS = RHS
Hence, the identity is proved.
(iii)
To Prove: $\frac{\tan \;θ}{1 \;-\; \cot \;θ} + \frac{\cot \;θ}{1 \;-\; \tan \;θ} = 1 + \sec θ \text{ cosec } θ$
Proof:
LHS = $\frac{\tan \;θ}{1 \;-\; \cot \;θ} + \frac{\cot \;θ}{1 \;-\; \tan \;θ}$
Express in terms of $\sin \theta$ and $\cos \theta$:
$= \frac{\frac{\sin \theta}{\cos \theta}}{1 - \frac{\cos \theta}{\sin \theta}} + \frac{\frac{\cos \theta}{\sin \theta}}{1 - \frac{\sin \theta}{\cos \theta}}$
Simplify the denominators:
$= \frac{\frac{\sin \theta}{\cos \theta}}{\frac{\sin \theta - \cos \theta}{\sin \theta}} + \frac{\frac{\cos \theta}{\sin \theta}}{\frac{\cos \theta - \sin \theta}{\cos \theta}}$
Rewrite the complex fractions:
$= \frac{\sin \theta}{\cos \theta} \times \frac{\sin \theta}{\sin \theta - \cos \theta} + \frac{\cos \theta}{\sin \theta} \times \frac{\cos \theta}{\cos \theta - \sin \theta}$
$= \frac{\sin^2 \theta}{\cos \theta (\sin \theta - \cos \theta)} + \frac{\cos^2 \theta}{\sin \theta (\cos \theta - \sin \theta)}$
Note that $\cos \theta - \sin \theta = -(\sin \theta - \cos \theta)$. Use this in the second term:
$= \frac{\sin^2 \theta}{\cos \theta (\sin \theta - \cos \theta)} + \frac{\cos^2 \theta}{-\sin \theta (\sin \theta - \cos \theta)}$
$= \frac{\sin^2 \theta}{\cos \theta (\sin \theta - \cos \theta)} - \frac{\cos^2 \theta}{\sin \theta (\sin \theta - \cos \theta)}$
Find a common denominator, which is $\sin \theta \cos \theta (\sin \theta - \cos \theta)$:
$= \frac{\sin \theta \times \sin^2 \theta - \cos \theta \times \cos^2 \theta}{\sin \theta \cos \theta (\sin \theta - \cos \theta)}$
$= \frac{\sin^3 \theta - \cos^3 \theta}{\sin \theta \cos \theta (\sin \theta - \cos \theta)}$
Use the algebraic identity $a^3 - b^3 = (a-b)(a^2 + ab + b^2)$ in the numerator, where $a = \sin \theta$ and $b = \cos \theta$:
$= \frac{(\sin \theta - \cos \theta)(\sin^2 \theta + \sin \theta \cos \theta + \cos^2 \theta)}{\sin \theta \cos \theta (\sin \theta - \cos \theta)}$
Cancel out the common term $(\sin \theta - \cos \theta)$ (assuming $\sin \theta - \cos \theta \neq 0$, i.e., $\tan \theta \neq 1$):
$= \frac{\sin^2 \theta + \cos^2 \theta + \sin \theta \cos \theta}{\sin \theta \cos \theta}$
Use the identity $\sin^2 \theta + \cos^2 \theta = 1$:
$= \frac{1 + \sin \theta \cos \theta}{\sin \theta \cos \theta}$
Separate the terms in the numerator:
$= \frac{1}{\sin \theta \cos \theta} + \frac{\sin \theta \cos \theta}{\sin \theta \cos \theta}$
$= \frac{1}{\sin \theta} \times \frac{1}{\cos \theta} + 1$
Use the reciprocal identities $\frac{1}{\sin \theta} = \text{cosec } \theta$ and $\frac{1}{\cos \theta} = \sec \theta$:
$= \text{cosec } \theta \sec \theta + 1$
$= 1 + \sec \theta \text{ cosec } \theta$
This is equal to the RHS.
LHS = RHS
Hence, the identity is proved.
(iv)
To Prove: $\frac{1 \;+\; \sec \;A}{\sec \;A} = \frac{\sin^2 \;A}{1 \;-\; \cos \;A}$
Proof:
We will simplify LHS and RHS separately.
Simplify LHS:
LHS = $\frac{1 \;+\; \sec \;A}{\sec \;A}$
Separate the terms in the numerator:
$= \frac{1}{\sec A} + \frac{\sec A}{\sec A}$
Use the reciprocal identity $\frac{1}{\sec A} = \cos A$:
$= \cos A + 1$
$= 1 + \cos A$
Simplify RHS:
RHS = $\frac{\sin^2 \;A}{1 \;-\; \cos \;A}$
Use the identity $\sin^2 A = 1 - \cos^2 A$ in the numerator:
$= \frac{1 - \cos^2 A}{1 \;-\; \cos \;A}$
Factor the numerator using $a^2 - b^2 = (a-b)(a+b)$:
$= \frac{(1 - \cos A)(1 + \cos A)}{1 \;-\; \cos \;A}$
Cancel out the common term $(1 - \cos A)$ (assuming $1 - \cos A \neq 0$, i.e., $\cos A \neq 1$):
$= 1 + \cos A$
Since simplified LHS = $1 + \cos A$ and simplified RHS = $1 + \cos A$, we have LHS = RHS.
Hence, the identity is proved.
(v)
To Prove: $\frac{\cos \;A \;-\; \sin \;A \;+\; 1}{\cos \;A \;+\; \sin \;A \;-\; 1} = \text{cosec } A + \cot A$, using the identity $\text{cosec}^2 A = 1 + \cot^2 A$.
Proof:
LHS = $\frac{\cos \;A \;-\; \sin \;A \;+\; 1}{\cos \;A \;+\; \sin \;A \;-\; 1}$
Divide the numerator and the denominator by $\sin A$ to get terms in $\cot A$ and $\text{cosec } A$ (assuming $\sin A \neq 0$):
$= \frac{\frac{\cos A}{\sin A} \;-\; \frac{\sin A}{\sin A} \;+\; \frac{1}{\sin A}}{\frac{\cos A}{\sin A} \;+\; \frac{\sin A}{\sin A} \;-\; \frac{1}{\sin A}}$
Substitute $\cot A = \frac{\cos A}{\sin A}$ and $\text{cosec } A = \frac{1}{\sin A}$:
$= \frac{\cot \;A \;-\; 1 \;+\; \text{cosec} \;A}{\cot \;A \;+\; 1 \;-\; \text{cosec} \;A}$
Rearrange the terms in the numerator:
$= \frac{(\cot \;A \;+\; \text{cosec} \;A) \;-\; 1}{(\cot \;A \;-\; \text{cosec} \;A) \;+\; 1}$
Use the identity $1 = \text{cosec}^2 A - \cot^2 A$ in the numerator:
$= \frac{(\cot \;A \;+\; \text{cosec} \;A) \;-\; (\text{cosec}^2 \;A \;-\; \cot^2 \;A)}{(\cot \;A \;-\; \text{cosec} \;A) \;+\; 1}$
Factor $\text{cosec}^2 A - \cot^2 A$ using $a^2 - b^2 = (a-b)(a+b)$:
$= \frac{(\cot \;A \;+\; \text{cosec} \;A) \;-\; (\text{cosec} \;A \;-\; \cot \;A)(\text{cosec} \;A \;+\; \cot \;A)}{(\cot \;A \;-\; \text{cosec} \;A) \;+\; 1}$
Take $(\cot A + \text{cosec } A)$ common from the numerator:
$= \frac{(\cot \;A \;+\; \text{cosec} \;A) [1 \;-\; (\text{cosec} \;A \;-\; \cot \;A)]}{(\cot \;A \;-\; \text{cosec} \;A) \;+\; 1}$
$= \frac{(\cot \;A \;+\; \text{cosec} \;A) [1 \;-\; \text{cosec} \;A \;+\; \cot \;A]}{1 \;-\; \text{cosec} \;A \;+\; \cot \;A}$
Cancel out the common term $(1 - \text{cosec } A + \cot A)$ (assuming it is not zero):
$= \cot \;A \;+\; \text{cosec} \;A$
This is equal to the RHS.
LHS = RHS
Hence, the identity is proved.
(vi)
To Prove: $\sqrt{\frac{1 \;+\; \sin \;A}{1 \;-\; \sin \;A}} = \sec A + \tan A$
Proof:
LHS = $\sqrt{\frac{1 \;+\; \sin \;A}{1 \;-\; \sin \;A}}$
Multiply the numerator and denominator inside the square root by $(1 + \sin A)$:
$= \sqrt{\frac{(1 \;+\; \sin \;A)(1 \;+\; \sin \;A)}{(1 \;-\; \sin \;A)(1 \;+\; \sin \;A)}}$
Simplify the numerator and the denominator:
$= \sqrt{\frac{(1 + \sin A)^2}{1^2 - \sin^2 A}}$
$= \sqrt{\frac{(1 + \sin A)^2}{1 - \sin^2 A}}$
Use the identity $1 - \sin^2 A = \cos^2 A$ in the denominator:
$= \sqrt{\frac{(1 + \sin A)^2}{\cos^2 A}}$
Take the square root of the numerator and the denominator:
$= \frac{\sqrt{(1 + \sin A)^2}}{\sqrt{\cos^2 A}}$
For acute angles A, $1 + \sin A$ is positive and $\cos A$ is positive, so $\sqrt{(1 + \sin A)^2} = 1 + \sin A$ and $\sqrt{\cos^2 A} = \cos A$.
$= \frac{1 + \sin A}{\cos A}$
Separate the terms in the numerator:
$= \frac{1}{\cos A} + \frac{\sin A}{\cos A}$
Use the reciprocal and quotient identities:
$= \sec A + \tan A$
This is equal to the RHS.
LHS = RHS
Hence, the identity is proved.
(vii)
To Prove: $\frac{\sin \;θ \;-\; 2\sin^3 \;θ}{2 \cos^3 \;θ \;-\; \cos \;θ} = \tan θ$
Proof:
LHS = $\frac{\sin \;θ \;-\; 2\sin^3 \;θ}{2 \cos^3 \;θ \;-\; \cos \;θ}$
Factor out $\sin \theta$ from the numerator and $\cos \theta$ from the denominator:
$= \frac{\sin \theta (1 \;-\; 2\sin^2 \;θ)}{\cos \theta (2 \cos^2 \;θ \;-\; 1)}$
We know that $\frac{\sin \theta}{\cos \theta} = \tan \theta$. So, we need to show that the terms in the parentheses are equal.
Use the identity $\sin^2 \theta = 1 - \cos^2 \theta$ in the numerator's parenthesis:
$1 - 2\sin^2 \theta = 1 - 2(1 - \cos^2 \theta)$
$= 1 - 2 + 2\cos^2 \theta$
$= 2\cos^2 \theta - 1$
So, the numerator becomes $\sin \theta (2\cos^2 \theta - 1)$.
Substitute this back into the LHS:
LHS = $\frac{\sin \theta (2\cos^2 \theta - 1)}{\cos \theta (2 \cos^2 \;θ \;-\; 1)}$
Cancel out the common term $(2\cos^2 \theta - 1)$ (assuming $2\cos^2 \theta - 1 \neq 0$):
$= \frac{\sin \theta}{\cos \theta}$
$= \tan \theta$
This is equal to the RHS.
LHS = RHS
Hence, the identity is proved.
(viii)
To Prove: $(\sin A + \text{cosec } A)^2 + (\cos A + \sec A)^2 = 7 + \tan^2 A + \cot^2 A$
Proof:
LHS = $(\sin A + \text{cosec } A)^2 + (\cos A + \sec A)^2$
Expand the squares using $(a+b)^2 = a^2 + 2ab + b^2$:
$= (\sin^2 A + 2 \sin A \text{ cosec } A + \text{cosec}^2 A) + (\cos^2 A + 2 \cos A \sec A + \sec^2 A)$
Use the reciprocal identities $\sin A \text{ cosec } A = 1$ and $\cos A \sec A = 1$:
$= (\sin^2 A + 2(1) + \text{cosec}^2 A) + (\cos^2 A + 2(1) + \sec^2 A)$
$= \sin^2 A + 2 + \text{cosec}^2 A + \cos^2 A + 2 + \sec^2 A$
Group $\sin^2 A$ and $\cos^2 A$ and use the identity $\sin^2 A + \cos^2 A = 1$:
$= (\sin^2 A + \cos^2 A) + 2 + 2 + \text{cosec}^2 A + \sec^2 A$
$= 1 + 4 + \text{cosec}^2 A + \sec^2 A$
$= 5 + \text{cosec}^2 A + \sec^2 A$
Use the identities $\text{cosec}^2 A = 1 + \cot^2 A$ and $\sec^2 A = 1 + \tan^2 A$:
$= 5 + (1 + \cot^2 A) + (1 + \tan^2 A)$
$= 5 + 1 + \cot^2 A + 1 + \tan^2 A$
$= 7 + \tan^2 A + \cot^2 A$
This is equal to the RHS.
LHS = RHS
Hence, the identity is proved.
(ix)
To Prove: $(\text{cosec } A – \sin A)(\sec A – \cos A) = \frac{1}{\tan \;A \;+\; \cot \;A}$
Proof:
We will simplify LHS and RHS separately.
Simplify LHS:
LHS = $(\text{cosec } A – \sin A)(\sec A – \cos A)$
Express in terms of $\sin A$ and $\cos A$:
$= \left(\frac{1}{\sin A} – \sin A\right)\left(\frac{1}{\cos A} – \cos A\right)$
Combine the terms within each parenthesis:
$= \left(\frac{1 – \sin^2 A}{\sin A}\right)\left(\frac{1 – \cos^2 A}{\cos A}\right)$
Use the identities $1 - \sin^2 A = \cos^2 A$ and $1 - \cos^2 A = \sin^2 A$:
$= \left(\frac{\cos^2 A}{\sin A}\right)\left(\frac{\sin^2 A}{\cos A}\right)$
Multiply the terms:
$= \frac{\cos^2 A \sin^2 A}{\sin A \cos A}$
Cancel out common terms $\sin A$ and $\cos A$ (assuming $\sin A \neq 0$ and $\cos A \neq 0$):
$= \cos A \sin A$
Simplify RHS:
RHS = $\frac{1}{\tan \;A \;+\; \cot \;A}$
Express $\tan A$ and $\cot A$ in terms of $\sin A$ and $\cos A$:
$= \frac{1}{\frac{\sin A}{\cos A} \;+\; \frac{\cos A}{\sin A}}$
Combine the terms in the denominator:
$= \frac{1}{\frac{\sin A \times \sin A + \cos A \times \cos A}{\cos A \sin A}}$
$= \frac{1}{\frac{\sin^2 A + \cos^2 A}{\cos A \sin A}}$
Use the identity $\sin^2 A + \cos^2 A = 1$ in the denominator's numerator:
$= \frac{1}{\frac{1}{\cos A \sin A}}$
Take the reciprocal of the denominator:
$= 1 \times (\cos A \sin A)$
$= \cos A \sin A$
Since simplified LHS = $\cos A \sin A$ and simplified RHS = $\cos A \sin A$, we have LHS = RHS.
Hence, the identity is proved.
(x)
To Prove: $\left( \frac{1\;+\;\tan^{2}\;A}{1\;+\;\cot^{2}\;A} \right)$ = $\left(\frac{1\;-\;\tan \;A}{1\;-\;\cot \;A} \right)^{2}$ = $\tan^2 A$
Proof:
This requires proving two equalities:
(1) $\left( \frac{1\;+\;\tan^{2}\;A}{1\;+\;\cot^{2}\;A} \right) = \tan^2 A$
(2) $\left(\frac{1\;-\;\tan \;A}{1\;-\;\cot \;A} \right)^{2} = \tan^2 A$
Proof of (1):
Consider the first part of the expression:
$\frac{1\;+\;\tan^{2}\;A}{1\;+\;\cot^{2}\;A}$
Use the identities $1 + \tan^2 A = \sec^2 A$ and $1 + \cot^2 A = \text{cosec}^2 A$:
$= \frac{\sec^2 A}{\text{cosec}^2 A}$
Express in terms of $\sin A$ and $\cos A$:
$= \frac{\frac{1}{\cos^2 A}}{\frac{1}{\sin^2 A}}$
$= \frac{1}{\cos^2 A} \times \frac{\sin^2 A}{1}$
$= \frac{\sin^2 A}{\cos^2 A}$
$= \left(\frac{\sin A}{\cos A}\right)^2$
$= \tan^2 A$
This proves the first equality: $\left( \frac{1\;+\;\tan^{2}\;A}{1\;+\;\cot^{2}\;A} \right) = \tan^2 A$.
Proof of (2):
Consider the second part of the expression:
$\left(\frac{1\;-\;\tan \;A}{1\;-\;\cot \;A} \right)^{2}$
Express $\cot A$ in terms of $\tan A$: $\cot A = \frac{1}{\tan A}$
$= \left(\frac{1\;-\;\tan \;A}{1\;-\;\frac{1}{\tan \;A}} \right)^{2}$
Simplify the denominator:
$= \left(\frac{1\;-\;\tan \;A}{\frac{\tan \;A \;-\; 1}{\tan \;A}} \right)^{2}$
Rewrite the complex fraction:
$= \left((1\;-\;\tan \;A) \times \frac{\tan \;A}{\tan \;A \;-\; 1} \right)^{2}$
Note that $\tan A - 1 = -(1 - \tan A)$.
$= \left((1\;-\;\tan \;A) \times \frac{\tan \;A}{-(1 \;-\; \tan \;A)} \right)^{2}$
Cancel out the common term $(1 - \tan A)$ (assuming $1 - \tan A \neq 0$, i.e., $\tan A \neq 1$):
$= \left(- \tan \;A \right)^{2}$
$= (-1)^2 (\tan A)^2$
$= 1 \times \tan^2 A$
$= \tan^2 A$
This proves the second equality: $\left(\frac{1\;-\;\tan \;A}{1\;-\;\cot \;A} \right)^{2} = \tan^2 A$.
Since both parts are equal to $\tan^2 A$, the given identity is proved.

